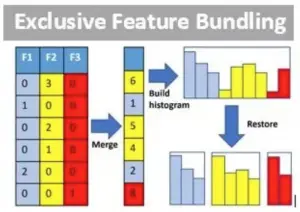
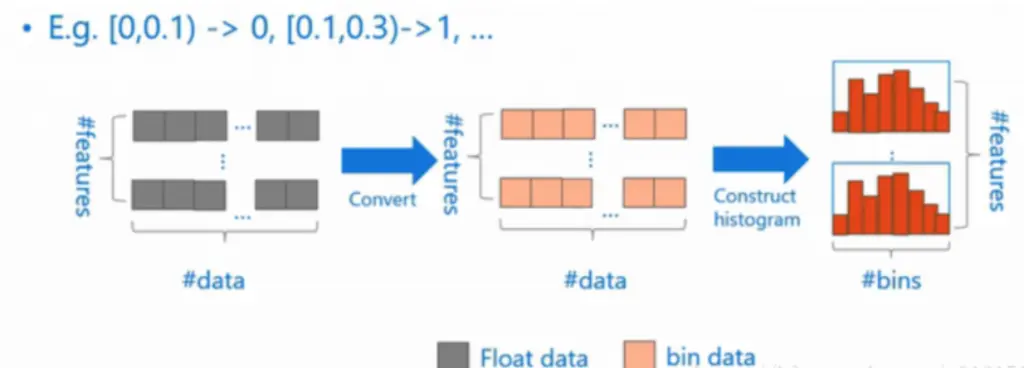
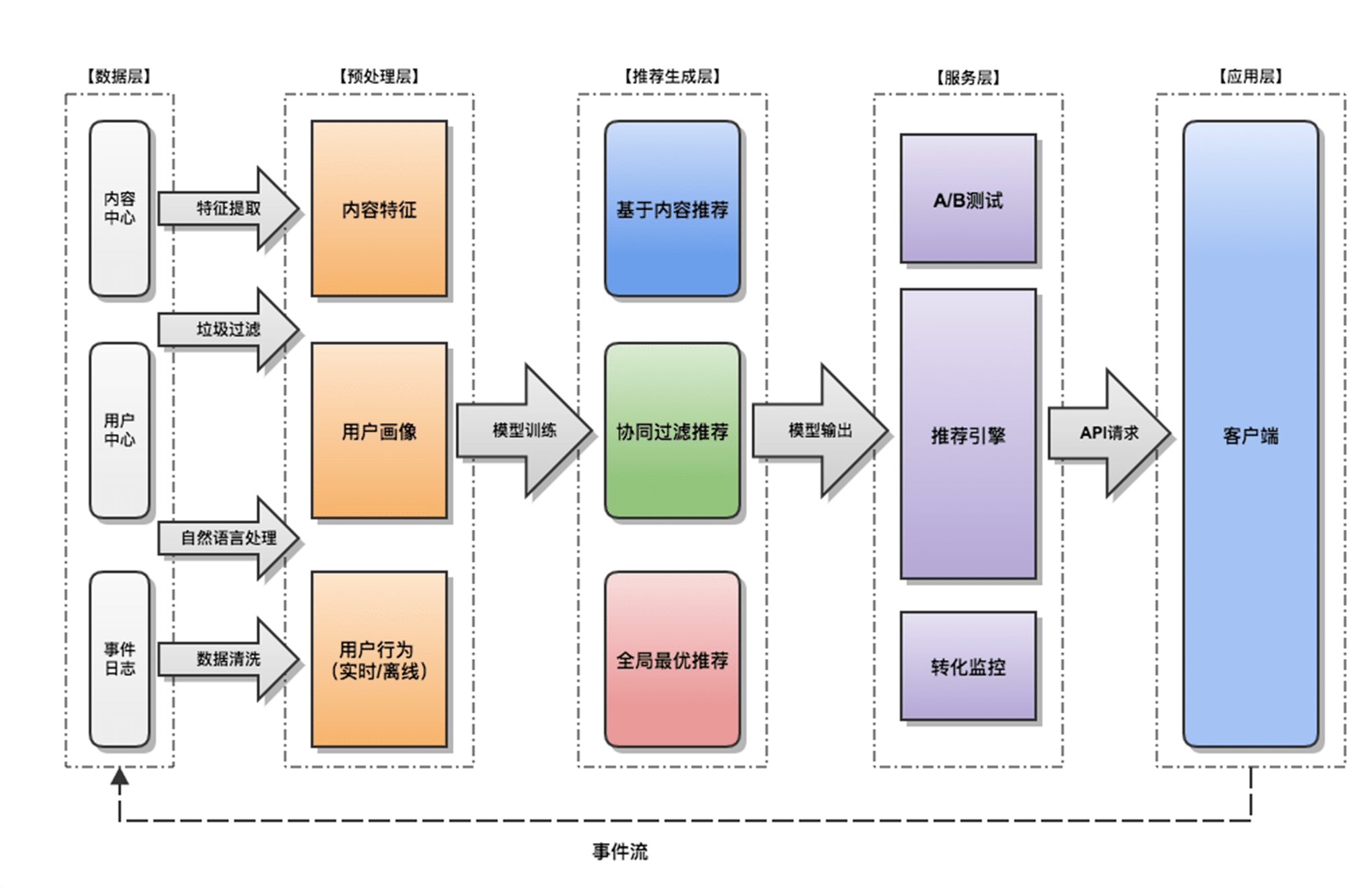
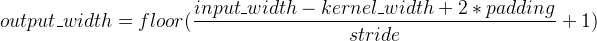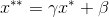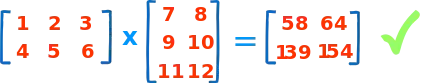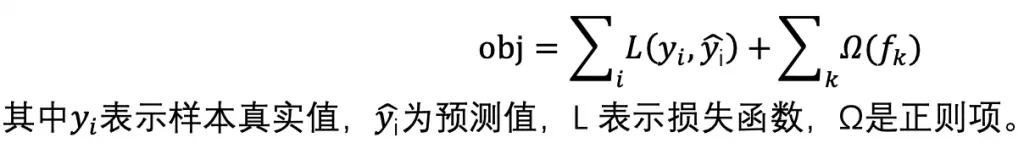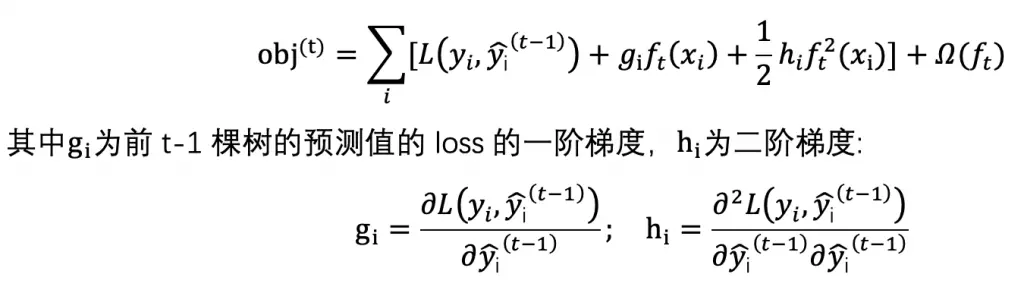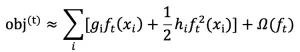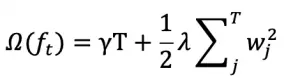CNN 的核心思想:局部感受野(local field) + 权值共享 + 亚采样 。

CNN 主要由四类层(layer)组成,即卷积层(Conv)、激活层(Activation)、池化层(Pooling) 以及全连接层(FC/Dense)。
卷积层(Convolution)
传统神经网络采用全连接的方式,往往容易导致需要训练的参数非常庞大,甚至难以训练,卷积神经网络通过卷积层的“局部连接”和“参数共享”的特性大大减少训练参数。
举例:输入 100 x 100, 隐藏层有10个神经元
传统全连接方式(Full Connected)
输入 100 x 100 与每一个神经元连接,需要训练 100 x 100 x 10 = 100000 个参数(不考虑bias)
局部连接(Sparse Connectivity)
假设每个神经元只与局部 10 x 10 个输入连接,那么只需要训练 10 x 10 x 10 = 1000 个参数!!
权值共享(Shared Weights)
如果每个神经元的连接使用相同的权值,那么实际训练参数进一步压缩到 10 x 10 x 1 = 100 个参数!!
卷积层如何生成
卷积核 (或称滤波器,filter/kernel)
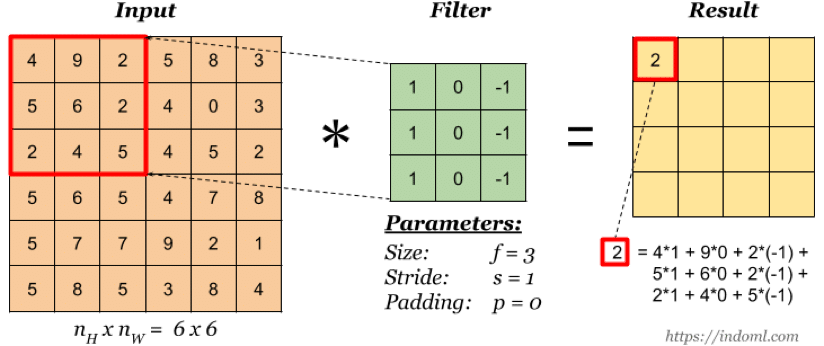
上图是一个尺寸为 3×3 的卷积核, 即每个神经元由输入的 3×3 局部连接所得,卷积核的值通过训练来学习。
卷积核的 stride 值
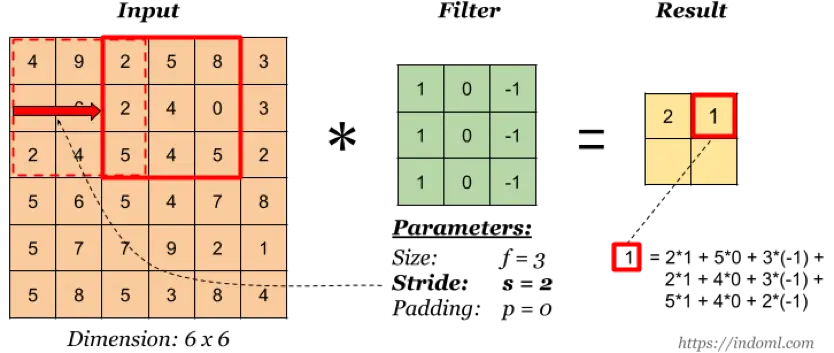
stride 指卷积核的移动步长(这其实就是权值共享的表现),上图 stride=2,卷积核每次移动两个单元。
卷积核的 padding 值
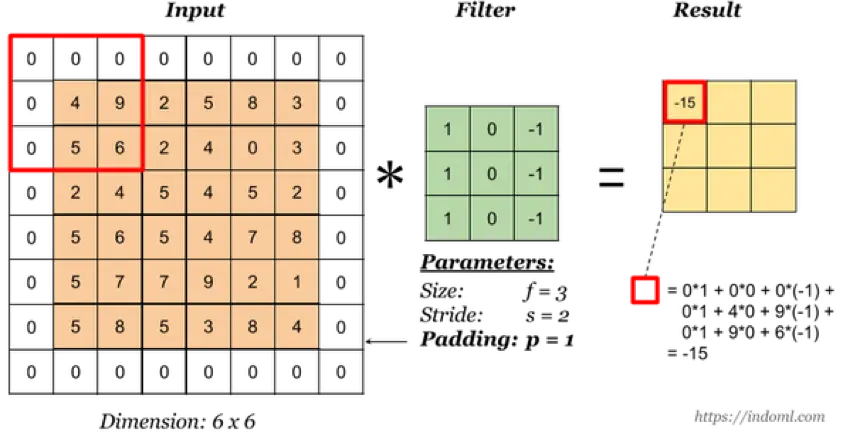
padding 即在输入矩阵的四周添加填充,一方面可以减少原输入的边缘影响,另一方面可以用于维持输入和输出的维度一致(需要 stride 配合)。
padding 的常见术语包括:
(1) valid: 即 no padding
(2) same:通过填充使得输入和输出的维度保持一致
卷积输出-Feature Map(特征图)
实际上卷积核的作用就是对输入层进行特征学习,卷积核可以看成是对输入的一种特征映射,通过这种特征映射,一个卷积核对应生成一个特征图(Feature Map),即上图的 Result。
多通道卷积
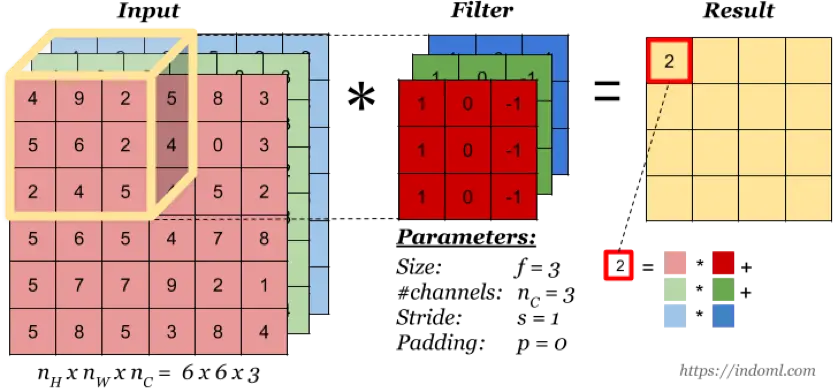
当输入有多个通道(channel)时(例如图片可以有 RGB 三个通道),卷积核需要拥有相同的channel数,每个卷积核 channel 与输入层的对应 channel 进行卷积,将每个 channel 的卷积结果按位相加得到最终的 Feature Map。
多卷积核
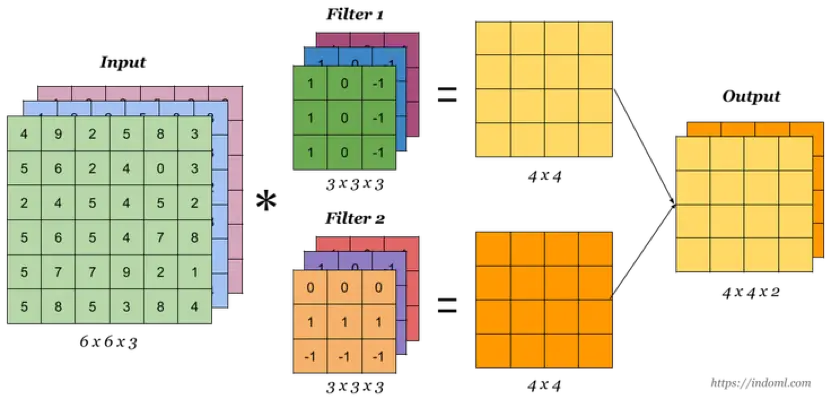
当有多个卷积核时,可以学习到多种不同的特征,对应产生包含多个 channel 的 Feature Map, 例如上图有两个 filter,所以 output 有两个 channel。
为什么不需要全连接而只需要局部连接就会有效果?
对于图像而言,局部区域的像素关联性往往很强,而相距较远的区域关联性往往很弱。同样,对于文本而言,相近的词汇在语义表达上往往有紧密联系而相隔较远的词汇语义关联则相对较低。因此,只需要对局部信息进行特征提取,最后综合起来就能达到全局感知。