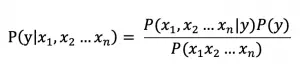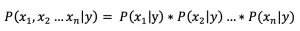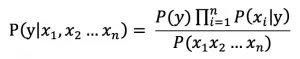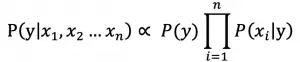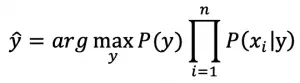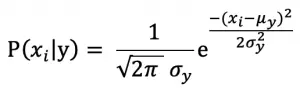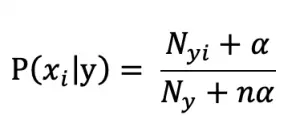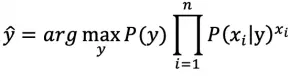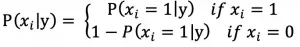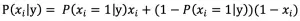朴素贝叶斯算法是一种基于贝叶斯理论的监督学习算法
对于一个含有n个特征(x1,x2 … xn)的样本,由贝叶斯理论可知它属于类y的概率为:
朴素贝叶斯算法假设特征之间是独立的,所以有:
因此有:
由于 P(x1 x2…xn ) 对所有类别是相同的,可以省略,即:
分别计算各个类别的概率,概率最大的类别则为最终的分类(最大后验概率),因此朴素贝叶斯算法最终表示为:
备注:P(y) 表示训练样本中类y的样本占比(先验概率)。
常见模型
朴素贝叶斯模型主要有三类常见的变形,即高斯模型、多项式模型以及伯努利模型。它们最大的不同在于对条件概率 P(x_i│y) 的计算差异,即对先验分布的假设不同。
高斯朴素贝叶斯模型(Gaussian Naive Bayes):
当特征是连续变量(身高、年龄)时,可以假设特征符合高斯分布,则
其中 μ_y 为类y样本中特征 x_i 的平均数,σ_y 为 y 类样本中特征 x_i 的标准差。
训练高斯模型实质是就是计算每个类别对应于特征的均值和标准差,例如:
{0:[(mean1, std1), (mean2, std2)], 1:[(mean1, std1), (mean2, std2)]}
多项式朴素贝叶斯(Multinomial Naive Bayes):
多项式模型可用于处理离散特征,例如:文本分类问题,特征 x_i 表示某个词在样本中出现的次数(当然用TF-IDF表示也可以)。条件概率计算公式为:
N_yi 表示类 y 的所有样本中特征 x_i 的特征值之和;
N_y 表示类 y 的所有样本中全部特征的特征值之和;
α 表示平滑值(α∈[0-1]),主要为了防止训练样本中某个特征没出现而导致 N_yi=0,从而导致条件概率 P(x_i│y)=0 的情况,如果不加入平滑值,则计算联合概率时由于某一项为 0 导致后验概率为 0 的异常情况出现。
n 表示特征总数。
多项式模型的预测公式为(即需要考虑出现次数的权重):
伯努利朴素贝叶斯(Bernoulli Naive Bayes):
伯努利模型的特征为布尔型,即只有1或者0两个取值,例如:在文本分类问题中,表示某个词是否出现在样本中。与多项式模型不同的是,多项式模型只考虑存在的特征,不存在的特征直接忽略条件概率的计算,而伯努利模型考虑的是全局特征,即使某个特征不存在,也会考虑不存在的可能性,条件概率计算公式为:
合并两式得:
伯努利模型适合处理短文本分类问题,因为相比计算某个词出现的次数,短文本往往对某个词是否出现更敏感。