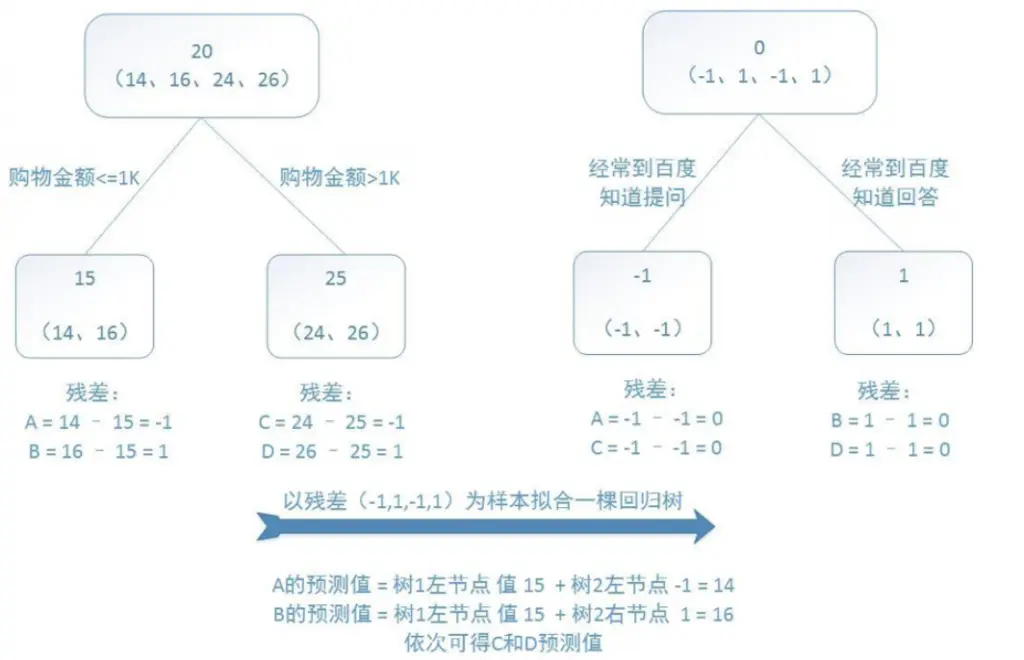
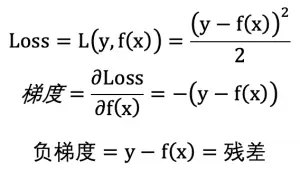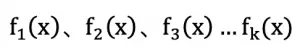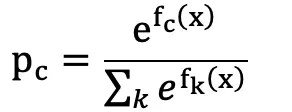GBDT 是一种以梯度提升(Gradient Boosting )作为训练策略,以回归决策树(Decision Tree,通常是 CART 回归树)作为弱模型的集成学习算法。其中梯度提升指每次迭代中通过拟合当前模型损失函数的负梯度(伪残差)来学习新的模型 ,从而通过结合新的模型使得模型损失进一步降低,而最终将多个模型结合的过程就是损失函数最小化的过程。
GBDT 分为 G、B、DT 三个部分
DT:即 decision tree 决策树,准确来说是回归树
B:即 boosting,指串行集成的模型结构
G:gradient,它通过拟合当前模型的损失函数的负梯度(残差)来学习新的模型
当以最小平方损失(LeastSquaresError)作为损失函数,此时损失函数的负梯度与残差(真实值 – 预测值)等价:
因此,每个弱模型的生成都是对前面所有模型的累加结果的残差的修正。
GBDT 原始论文算法描述
第 2.3 步算法复杂度较高,通常不使用 line search,而是指定一个很小的值,即 shrinkage。
关于 Shrinkage(缩减因子)
每棵树累加时都要乘以缩减因子,相当于为每棵树设置了权重,也就是每次只学习一部分的残差或换句话说每次只沿着负梯度方向前进一小步,相当于学习率 / 步长,能减少过拟合(实际上是一种正则化方法)。
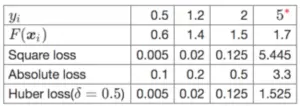
不同损失函数的区别
yi=5 为异常点
不同损失函数对异常值的敏感度不同,常用的平方损失函数,往往对异常点非常敏感,因此基于残差的 GBDT 可能不是一个好的选择(鲁棒性不好)
为什么 GBDT 是回归树,而不是分类树?
分类树的结果是类别,而类别相加是没有意义的,只有回归树的结果相加才有意义,由于 GBDT 每次迭代生成的回归树是通过对损失函数的负梯度进行拟合所构建的,所以实际上 GBDT 的回归树相加的过程就是梯度下降优化的过程。
注意:GBDT 因为用了回归树,所以分裂指标是均方误差最小,而不是基尼指数!!!
GBDT 如何应用于分类问题
- 在回归问题中,GBDT 每一轮迭代都构建了一棵树,实质是构建了一个函数 f,当输入为 x 时,树的输出为 f(x)。
- 在多分类问题中,假设有 k 个类别,那么每一轮迭代实质是构建了 k 棵树(相当于转化成 k 个二分类问题),对某个样本 x(样本表示 {x, 1 or 0})的预测值为
通过 Softmax(对于二分类问题可用 sigmoid 计算)转换为概率表示,则对于某个类别 c 有:
此时即可以通过 logloss 作为损失函数,并计算 f1(x) ~ fk(x) 的 loss function 负梯度值(伪残差)供下一轮迭代学习
3. 最终预测时,输入 x,得到 k 个输出,通过 Softmax 计算各类别的概率即可。
AdaBoost vs GBDT 区别
AdaBoost 每轮迭代通过调整样本分布,即不同样本具有不同的权重,使得学习的基模型更关心预测困难的样本。将多个基模型结合成强模型时,根据不同基模型的误差表现分配不同的加权系数,误差越低权重越高。
GBDT 每轮迭代无需调整样本权重分布,而是通过拟合当前模型损失函数的负梯度(伪残差)构建新的基模型。将多个基模型直接相加得到最终的强模型,实际就是一个梯度下降优化的过程。
GBDT vs 随机森林区别
相同点:
1. 都是由多棵树组成的集成学习算法
不同点:
1. 模型结构:随机森林的树模型可以是回归树也可以是分类树,GBDT 的树模型通常由回归树组成(也许有变体,但没有接触过)
2. 训练方式:随机森林可以并行训练,GBDT 只能串行训练(树粒度串行,特征粒度可以并行,例如 xgboost 实现)
3. 模型倾向:随机森林倾向于通过降低方差(随机抽样,随机特征带来的泛化能力的提升)来提升模型性能,GBDT 倾向于通过降低偏差(迭代学习残差使得模型对训练样本的拟合程度得到提升)来提升模型性能
优点
- 非线性表达能力强,精确度较高
- 能处理连续特征和离散特征
- 对特征伸缩不敏感(无需归一化)
- 可解释性强
缺点
- 多分类问题复杂度较高(实际构建 n_classes * n_estimators 棵树)
- 并行训练比较困难
- 不适合高维稀疏特征
主要调优参数
- 树的深度
- 树的数目
- 损失函数
- 缩放因子