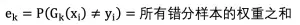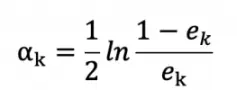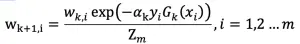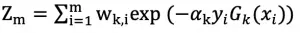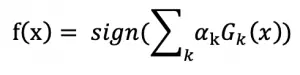通过结合多个模型来完成学习任务,生成更强大的模型,相比单一模型,集成学习往往具有更好的泛化能力。根据结合的模型的类型是否相同(是否由相同算法生成),可以分为同质和异质。
根据结合方式的不同,集成学习可以分为两大类
模型之间不存在强依赖关系,可以并行训练,例如:Bagging、Random Forest
模型之间存在强依赖关系,必须串行化训练,例如:AdaBoost
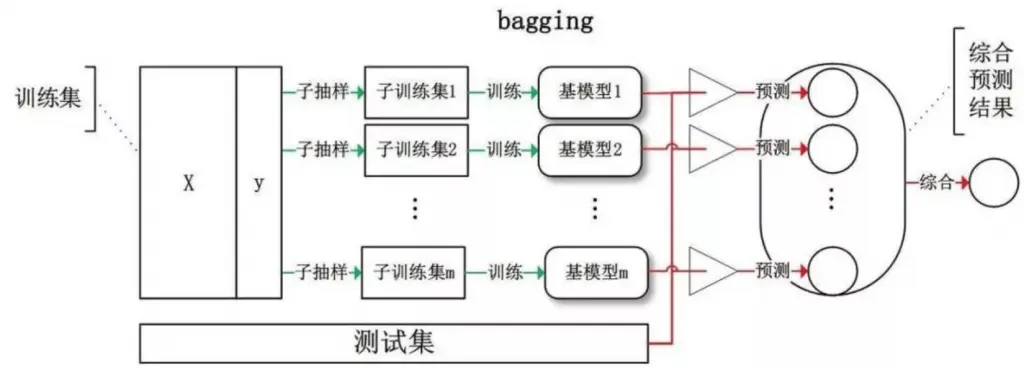
Bagging(并行集成)
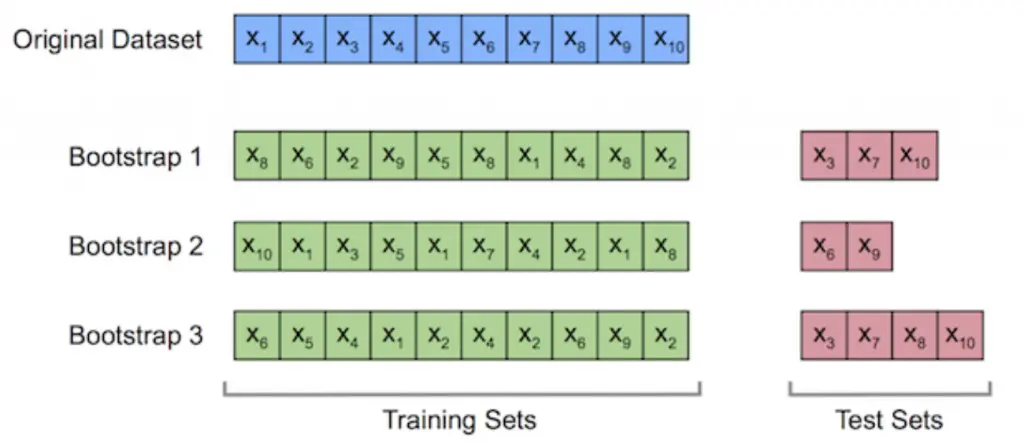
- 为了保证每个基模型的差异(集成学习的关键,样本差异可以使得模型关注不同角度),每个模型的训练集通过自助采样(.632 Bootstrap 采样)的方式生成 。
自助采样:等概率 、 有放回地从训练集中抽取 n 个样本作为训练集(相同样本可能出现多次),其余没有被抽到的样本作为测试集,原始训练集的 63.2% 的样本会出现在训练集中。
- 输出预测方式:投票法(分类),平均法(回归)
- 优点:
由于多个模型可以并行训练,所以训练比较高效 ;
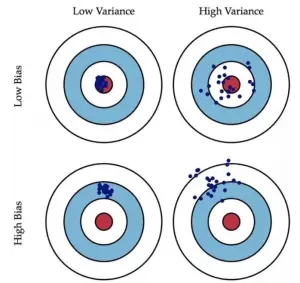
结合多个模型的预测能力,能有效提升泛化能力(即更低的方差 low variance)
Bias:训练样本准确率(更复杂的模型)
Variance:测试样本的准确率(泛化能力,更简单的模型)
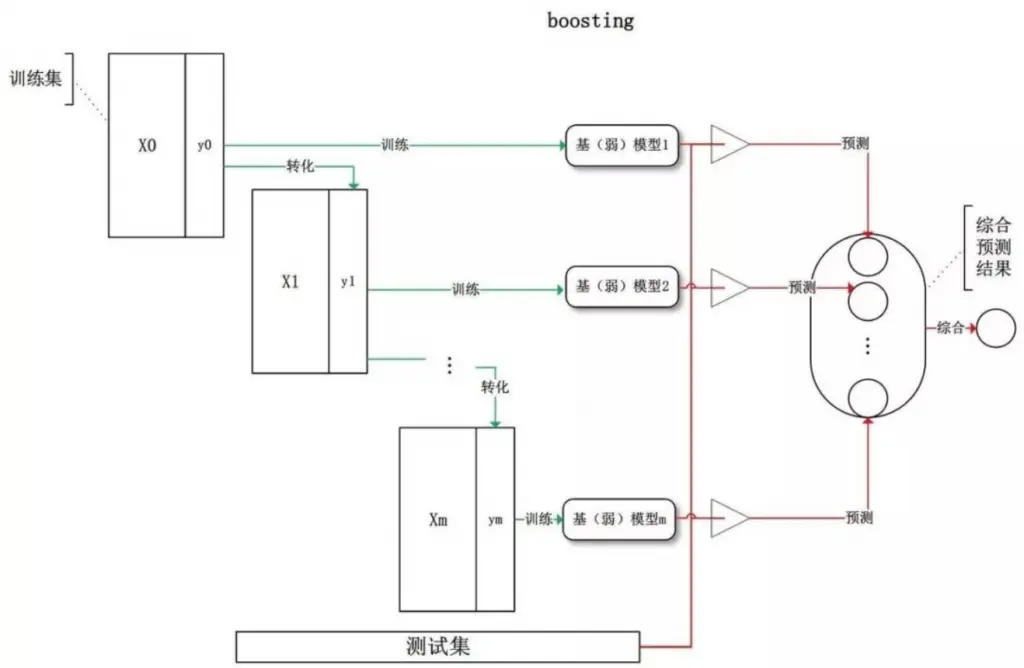
Boosting(串行集成)
- 从初始训练集学习一个基模型。
- 根据上一个基模型的表现调整训练样本的分布(增加误分样本的权重,降低正确分类样本的权重)。
- 基于新的样本分布初始化新的训练集(误分样本更被重视)训练新的基模型。
- 重复以上步骤直到生成 T 个模型,通过加权线性结合所有基模型并进行预测。
- 偏向降低模型偏差(bias)
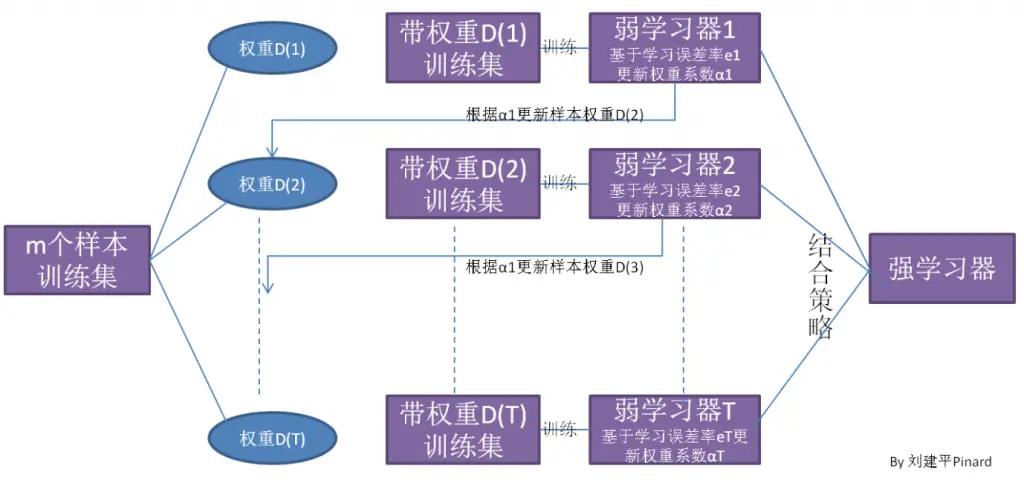
AdaBoost
以二分类为例
1. 输入样本集 T = {(x1,y1), (x2, y2) …… (xm, ym)}, 输出为 {-1, 1}, 弱分类器(例如 CART 决策树),迭代次数 k 次
2. 初始化样本集权重 D1(w11,w12 … w1m),每个样本的初始化权重为 1/m
3. 对于 k=1,2,3 … k, 使用样本权重为 Dk 的训练集训练弱分类器 Gk(x)
4. 计算 G_k (x)的分类误差率:
例如:a,b,c 样本分类错误,对应权重均为 0.1,则误差率为 0.3
5. 计算弱分类器的权重系数:
可知,当误差率越大,弱分类器的权重系数就越小。(这个公式由指数损失函数求导所得,实际上最小化指数损失函数等价于最小化类误差)
6. 更新样本集的权重分布:
其中 Z_m 为归一化因子,使得样本集权重满足概率分布:
当 yi*Gk(xi)为正时,即同号,表示分类正确,反之分类错误,所以分类正确的样本,权重降低,分类错误的样本权重增大。
7. 重复 3-6 步骤,训练 k 个弱分类器。
8. 强分类器生成:
优点
- 处理分类问题时,精度较高
- 可以通过各种分类回归模型构建弱学习器,比较灵活
- 不容易过拟合(经验证明,没有理论证明)
缺点
- 对异常样本敏感,异常样本在迭代学习中可能会获得较高权重,影响最终生成的强模型的准确性
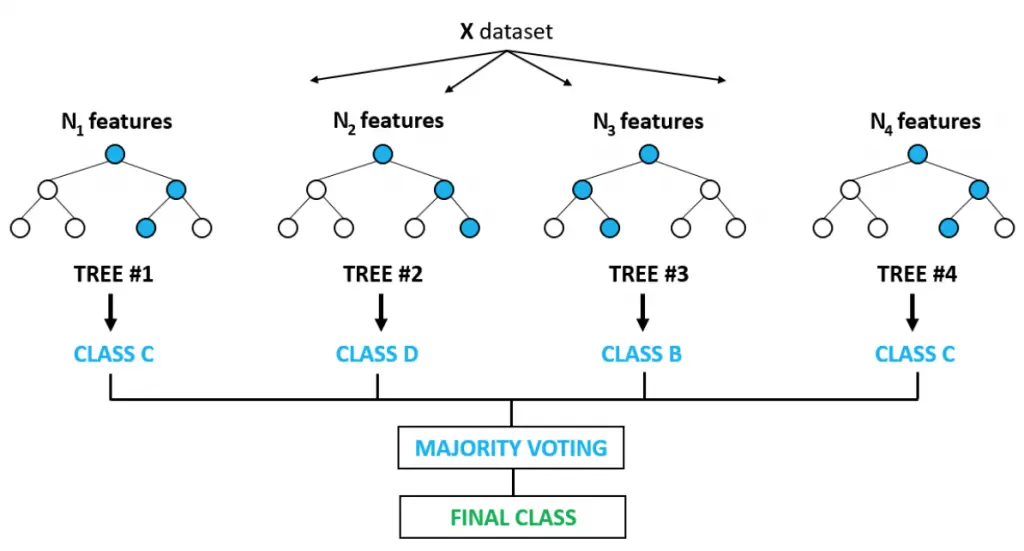
随机森林(Random Forest)
随机森林算法是一种 Bagging 算法的变体,它与 Bagging 最大的不同在于随机森林引入了随机特征选择。因此随机森林算法可以概括为以下步骤:
1. 随机选择样本(Bootstrap 采样)
2. 随机选择部分特征作为样本特征
3. 构建决策树(只能从随机选择的特征集中选择最优的划分特征)
4. 模型结合(投票法 、 平均法)
说明:随机选择特征会稍微增大单棵树偏差(bias),但会降低方差(variance),即提升泛化能力,从总体而言,随着学习器的增多,最终生成的模型会更好。
优点
- 由于每次只考虑部分特征,因此计算效率比较高
- 两个随机性的引入(样本 、 特征),不容易过拟合,抗噪能力强
- 能处理高维数据
缺点
- 对于噪音较大的数据集容易过拟合