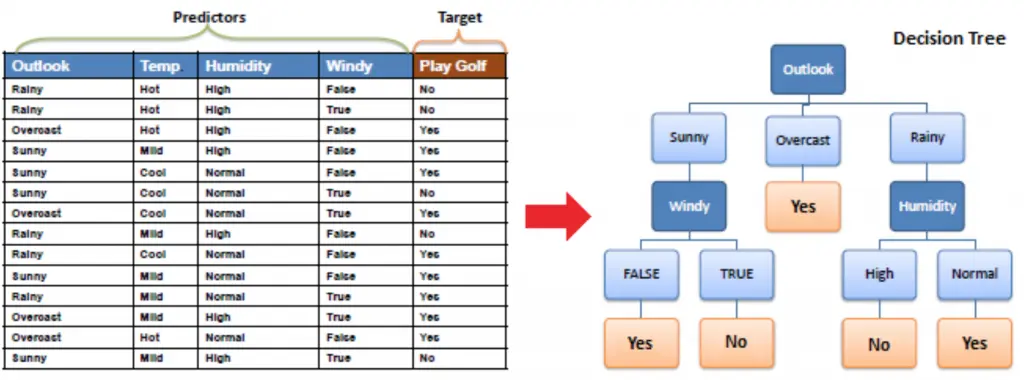
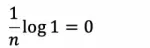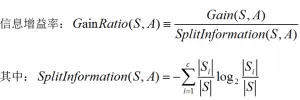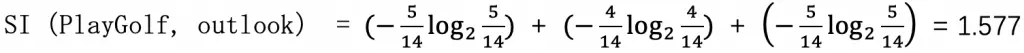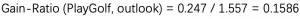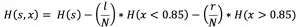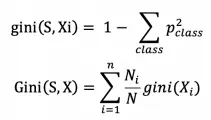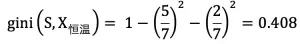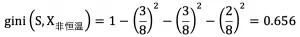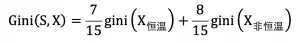决策树是一种非参数的监督学习算法,用于分类和回归任务,具有很强的解释性。决策树算法通过学习训练样本的特征,构建树状决策模型,最终生成一系列决策规则用于预测。
ID3 ( 信息增益, 分类算法,只支持类别特征,多叉树结构 )
特征选择准则
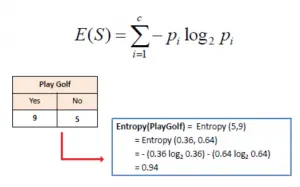
信息熵 : 随机变量 Y 的不确定程度
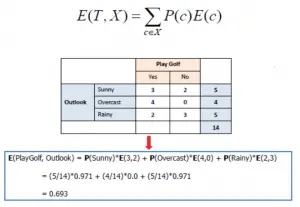
条件熵 : 在某一条件 X 的限制下,随机变量 Y 的不确定程度
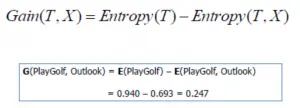
信息增益 (Information Gain): 条件 X 减少随机变量 Y 的不确定性的程度
信息增益 = 信息熵 – 条件熵
说明 : 是否 PlayGolf 这件事的不确定性为 0.940,如果知道 outlook 的话,那么这种不确定性会减少 0.247
ID3 决策树构建步骤
- 计算每个特征的信息增益
- 选择信息增益最大的特征作为决策树的节点,并根据其特征取值分裂出分支节点
- 如果分支节点的熵为 0( 即该节点的分类决策完全一致 ),则该节点为叶子节点,如果熵大于 0,则继续分裂。
- 重复 1-3 的步骤,直到所有特征的信息增益小于阈值或没有特征可用为止。
ID3 算法只有树的生成,所以该算法产生的树容易过拟合。
C4.5 ( 信息增益率,分类算法,支持类别特征 + 连续特征,多叉树结构 )
C4.5 是对 ID3 的一种改进,ID3 使用信息增益作为特征选择准则,但信息增益有一个缺点,它偏向于选择特征取值种类多的特征,即特征取值种类多的特征信息增益往往比较大。例如,以身份证号码作为特征,由于每个样本的身份证号码都是唯一的,每个取值只有一个样本,一个分类,所以每个取值的条件熵为:
那么信息增益会被最大化,但这种特征显然不是合理的分裂节点,因为通过已知的身份证号码来预测未知用户显然是不可取的。
信息增益率 (Gain-Ratio)
c4.5 采用信息增益率作为特征选择的准则
例如 :outlook 特征取值为 sunny(5 个 ), overcast(4 个 ), rainy(5 个 ),总样本数 14 个,则 outlook 这个特征的分裂信息为 :
信息增益率为 :
启发式特征选取
信息增益率偏向于选择特征取值种类数较少的特征 ( 某个 Si 趋向于 S 时,分裂信息接近 0,信息增益率会非常大 ),可以通过启发式策略,先选取信息增益大于平均值的特征,再从这些特征中选取信息增益率最大的特征作为分裂节点。
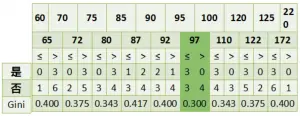
连续特征处理
处理连续特征首先需要对连续特征进行离散化处理,即设定一个阈值分割连续特征,使其成为二类特征,而关键点在于如何选择合适的分割阈值。
1. 对连续特征的所有取值进行排序
2. 分别选取每两个取值之间的中点作为候选分割点。如果有 n 种取值,则有 n-1 个候选分割点
3. 计算不同分割方式的信息增益,信息增益最大的分割点作为最优分割点,并计算该分割方式下的信息增益率作为该特征的信息增益率。
例如:
连续特征 :0.5, 1.2, 3.4, 5.4, 6.0
以 (0.5 + 1.2)/ 2 = 0.85 作为分割点,计算信息增益 :
其中 l 是分割点左边的样本数,r 是分割点右边的样本数,N 是样本总数.
以 (1.2+3.4) / 2 = 2.3 作为分割点,计算信息增益 … 以此类推
CART( 基尼指数,分类 、 回归算法,支持类别特征和连续特征,二叉树结构 )
CART (Classification And Regression Tree) 分类回归树,可用于分类和回归问题。
基尼指数
对于分类树,特征选择的准则为基尼指数 ( 基尼不纯度 ),它衡量随机变量被错误分类的可能性,或从数据集中随机抽取两个样本,它们的类别不一致的可能性,因此基尼指数越低,特征划分能力越好。
Xi 表示特征 X 的第 i 个取值,p_class 表示样本属于分类 class 的概率,N_i 表示特征 X 第 i 个取值的样本数,N 表示总样本数。Gini(S,X) 表示集合 S 按照特征 X 划分为多个集合后,其不确定性的大小。
例如 : 有 15 个样本,以体温为特征分为恒温和非恒温。
X_ 恒温时包含 7 个样本,Y_ 哺乳类 5 个 、Y_ 鸟类 2 个:
X_ 非恒温时包含 8 个样本,Y_ 爬行类 3 个 、Y_ 鱼类 3 个 、Y_ 两栖类 2 个 :
则集合 S 通过特征 X 划分后的基尼指数为 :
基尼指数 Gini 越小的特征越优先作为构建树节点的划分特征。
说明 : 基尼指数和熵其实都是一种不确定性的度量方式,CART 采用基尼指数作为特征选择的准则的好处是计算效率更高,因为熵的计算往往涉及大量的 log 运算。
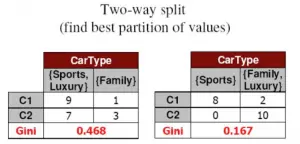
多值离散特征处理
CART 是一棵二叉树,即每个划分节点只有两个分支,如果离散特征有 3 个或以上的可取值,则需要对特征进行超类组合 ( 双化 ),计算不同组合下的基尼指数 ( 即划分为 X=a 和 X!=a 的组合,类似于 one vs rest),取基尼指数最小的组合作为最优超类组合,例如 :
连续特征处理
实际上与 C4.5 处理连续特征的方式一致,度量准则为基尼指数。
CART 分类树递归构建
CART 是一棵二叉树,每次选出最优的特征进行分裂使得子节点的数据尽可能纯,且只分裂为两个分支 ( 一个分支为特征 X=a, 另一个分支为特征 X!=a),在两个分支上重复相同步骤,重新选取最优特征并对子节点数据进行分裂,递归处理。
注意 :ID3/C4.5 构建树时,特征不能在后面复用 ( 因为是多叉树 ),导致划分过于迅速,而 CART 由于是二叉树,所以特征可以在子集中复用,即可以选择相同特征的不同特征值继续分裂。
CART 回归树生成
回归树基于平方误差最小化作为准则对数据进行划分。
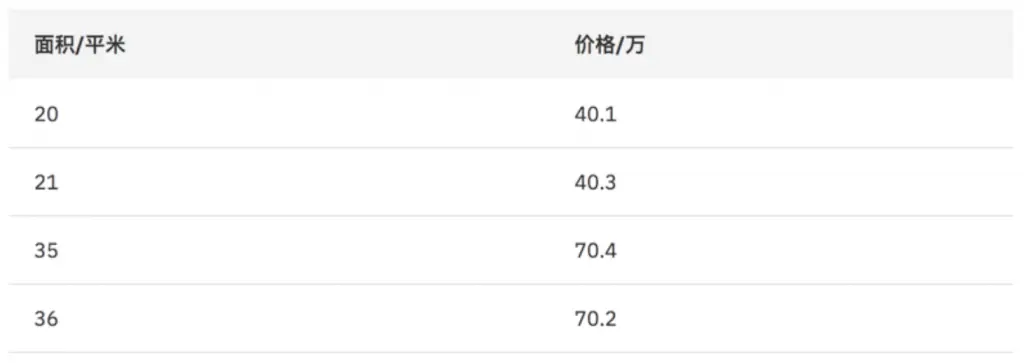
1. 计算每个特征的最优切分点 :
按特征 “面积=20”划分数据集 ( 面积 <=20, 面积 >20)
y1 均值为 40.1 ,
y2 均值为 (40.3+70.4+70.2)÷3 =60.3
平方误差: (40.1-40.1)^2+(40.3-60.3)^2+(70.4-60.3)^2+(70.2-60.3)^2=600.02
同理 :
按特征 “面积=21”划分数据集,平方误差 :0.04
按特征 “面积=35”划分数据集,平方误差 :608.05
按特征 “面积=36”划分数据集,平方误差 :608.05
所以最优切分点为 “面积=21”,即以面积作为划分特征的平方误差为 0.04
2. 计算所有特征的平方误差,选择误差最小的特征作为分裂特征 ( 上例只有一个特征 )。
3. 分裂后得到两个子节点,如果节点满足停止条件 ( 例如平方误差足够小 ) 则不再分裂,该节点变为叶子节点,节点值为样本的平均值,否则重复 1-2 步骤继续递归构建。
停止条件 ( 预剪枝 )
- 节点样本数少于预定阈值
- 节点样本集的基尼指数 ( 信息增益 、 信息增益率 、 平方误差 ) 小于预定值 ( 即分裂增益小 )
- 没有更多特征
- 达到最大深度
过拟合解决 ( 剪枝 / 后剪枝 ):
由于决策树是基于训练数据最大化度量准则而生成的,往往会生成出复杂度非常高且对训练数据预测非常准确的模型,但对未知数据的预测能力也往往非常差,容易存在过拟合问题。解决过拟合问题常用的方法是剪枝 (pruning),本质上是一个正则化过程。通过从已生成的树上剪掉一些子树并将它的根节点作为叶子节点,从而简化模型。剪枝并不是随意裁剪,而是基于最小化损失函数的方式进行裁剪。
决策树的损失函数定义为:
其中红色项表示模型的预测误差,蓝色项表示模型复杂度,α 是正则化参数用于衡量两者,α 越大模型越简单,反之模型越复杂 ( 过拟合可能性越大 )。
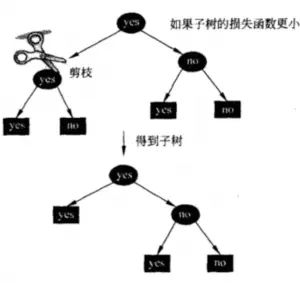
REP(Reduced Error Pruning, 错误率降低剪枝 ) 剪枝过程:
1. 递归地从叶子节点往上回缩,回缩后原来的父节点成为叶子节点。
2. 计算回缩前后两课树的损失函数值,如果回缩后损失减少,则进行剪枝。
例如:
总结
决策树算法主要包括三个部分:
特征选择 、 树的生成 、 树的剪枝
特征选择的关键是准则:
信息增益 、 信息增益比 、Gini 指数
决策树的生成:
利用信息增益最大 、 信息增益比最大 、Gini 指数最小作为特征选择的准则。从根节点开始,递归的生成决策树。相当于不断选取局部最优特征,将训练集分割为基本能够正确分类的子集 ;
决策树的剪枝:
决策树的剪枝是为了防止树的过拟合,增强其泛化能力。包括预剪枝和后剪枝。
优点:
- 解释性强,决策规则符合人的习惯思维逻辑
- 需要调优的超参数较少
- 能表达特征的重要性
- 能学习非线性关系
缺点:
- 非常容易过拟合 ( 通过剪枝解决 )