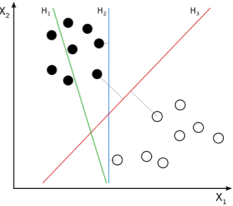
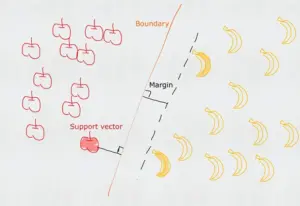
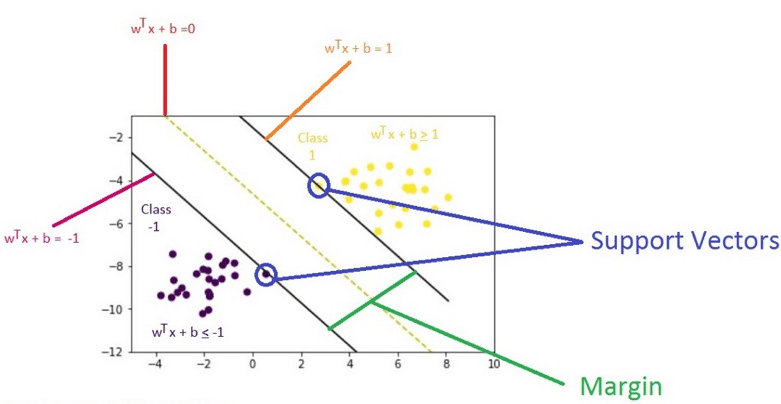
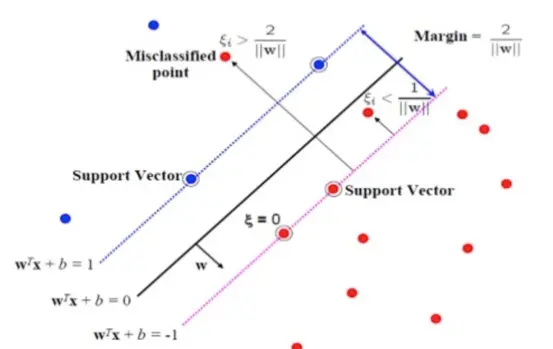
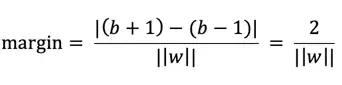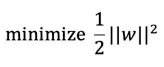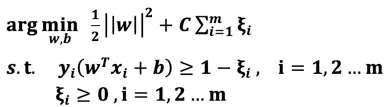SVM是一种二元分类模型(当然它也可以处理回归问题),它通过训练样本寻找分隔两类样本的最优决策边界(超平面),使得两类样本距离决策边界的距离最远(例如H3)。其中距离决策边界最近的样本称为支持向量(即深色的苹果和香蕉),支持向量所在的与决策平面平行的平面称为支撑平面(虚线),支撑平面与决策平面的距离称为间隔(margin),SVM寻找最优决策边界实际上就是要最大化(最大可信度)两个支撑平面的间隔(决策平面位于两者的中间)。
SVM 模型根据数据集的差异可以分为三种类型:
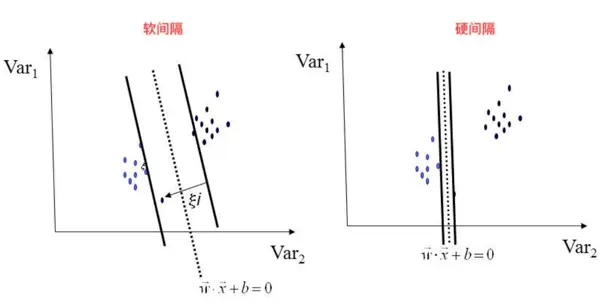
- 线性可分 => 硬间隔最大化 => 线性可分SVM
- 线性不可分(有噪音)=> 软间隔最大化 => 线性 SVM(引入松弛变量和惩罚函数)
- 非线性可分 => 软间隔最大化 + 核函数 => 非线性 SVM
一、线性可分(硬间隔最大化)
假设决策超平面为: W·X + b = 0
正类支撑平面为: W·X + b = γ
由对称关系可知负类支撑平面为: W·X + b = -γ
由于平面等比例缩放依然属于同一平面, 即 5W·X + 5b = 5 与 W·X + b = 1 是同一个平面
所以前面的假设可以更简洁地表示为(按γ等比例缩放):
决策平面: W·X + b =0
正类的支撑平面: W·X + b = 1
负类的支撑平面: W·X + b = -1
要求满足以下规则:

计算两个支撑平面的距离(margin)
由两平面距离公式可知,平面 W·X + b + 1 = 0 与平面 W·X + b -1 = 0的距离为:
所以要最大化margin相当于要最小化 ||w|| 即等价于:
最终的优化问题(目标函数)变成:
二、线性不可分(软间隔最大化)
当训练数据含有噪音数据时,如果进行硬间隔最大化可能会导致间隔过小甚至无法求解。
此时我们引入松弛变量(Slack Variable)ξ (epsilon ξ≥0) ,将原来的不等式约束变为:
松弛变量相当于为支撑平面提供了一个容错的区间,允许噪音数据存在(误分类样本),当松弛变量越大那么容错范围越大,反之,当ξ=0,等价于硬间隔最大化。当然我们不能无限制地容错,为了调和“间隔最大化”和“区分最大化”我们引入惩罚参数C,目标函数变成:
说明:相当于将“经验风险最小化问题”转变为引入了置信风险的“结构风险最小化问题”
说明:ξ_i≥0 与 hinge loss:max(0,1-y_i (w^T x_i+b)) 实际上是等价的。
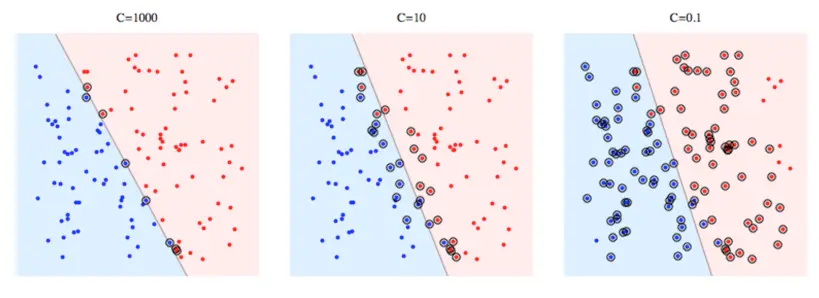
当C 越大,模型对误分类的惩罚越大,相当于分类更精确,但同时会牺牲间隔距离,可能导致过拟合。
当C 越小,模型对误分类的惩罚越少,相当于更倾向于间隔距离最大化以提升泛化能力,但同时牺牲了分割性,可能导致欠拟合。