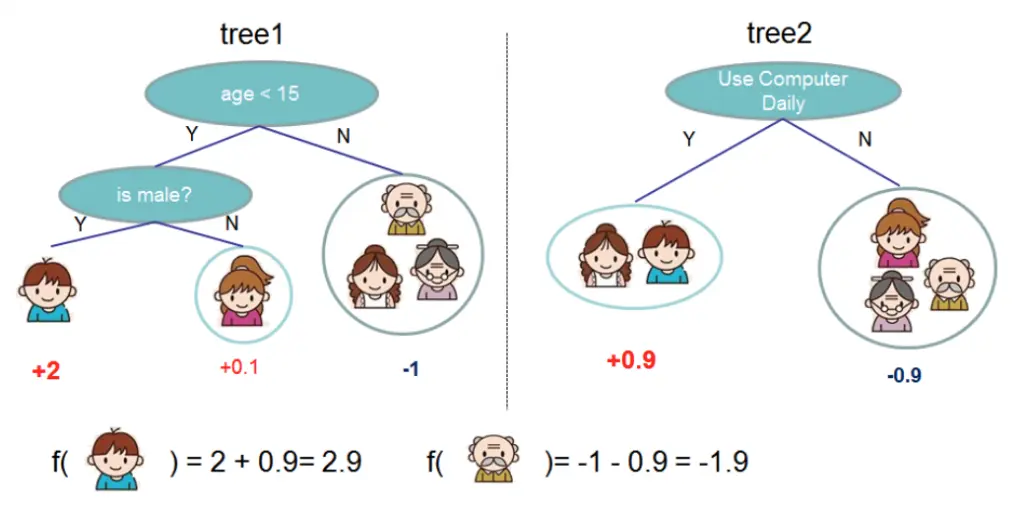
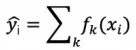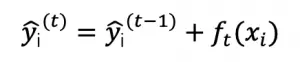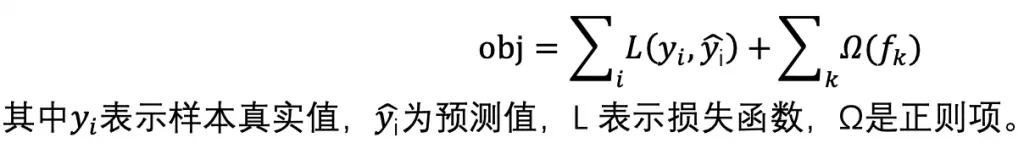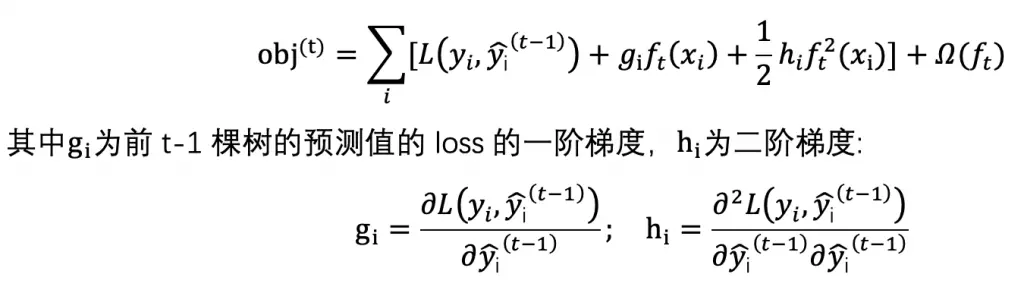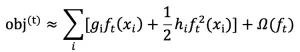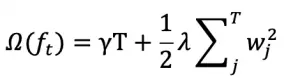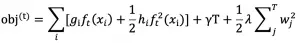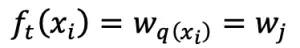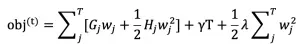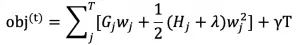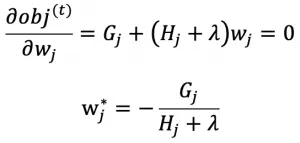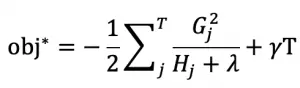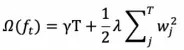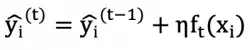xgboost 是对传统 GBDT 算法的一种改进实现,主要包括损失函数 、 正则化 、 分裂点查找优化 、 稀疏特征感知 、 并行化等方面.
原理推导
假设迭代训练 k 次,那么 xgboost 的模型函数可以表示为:
其中 k 表示决策树的数目,f 表示一棵 CART 树。那么,前 t 棵树的预测值可以表示为:
需要优化的目标函数为:
那么训练第 t 棵树的目标函数可表示为:
在前 t-1 棵树处进行二阶泰勒展开:
由于去除常数项 L 后不影响问题优化,因此目标函数化简为:
xgboost 定义正则项如下:
其中 T 为叶子数,wj 为第 j 个叶子节点的预测值(权重,prediction score)。目标函数为:
对于样本 xi ,在第 t 棵树的预测值表示为:
其中 q 表示树结构, q(xi) 表示样本 xi 在中被分到的叶子节点索引,wj 表示第 j 个叶子节点的预测值,因此原目标函数由样本表示形式(sample-wise)改写成树结构表示形式(structure-wise):
化简得:
其中 Gj 和 Hj 分别表示被分到第 j 个叶子节点的所有样本的 loss 的一阶(二阶)导数值之和,wj 表示第 j 个叶子节点的预测值(权重),T 表示叶子节点数。
对目标函数求关于 wj 的导数等于 0 即可得最优的预测值 wj^* 使得目标函数最小化:
将 wj^* 代入目标函数 obj^(t) 得 xgboost 的终极目标函数:
上式度量了一棵结构为 q(x) 的树的好坏,值越小越好!!!!
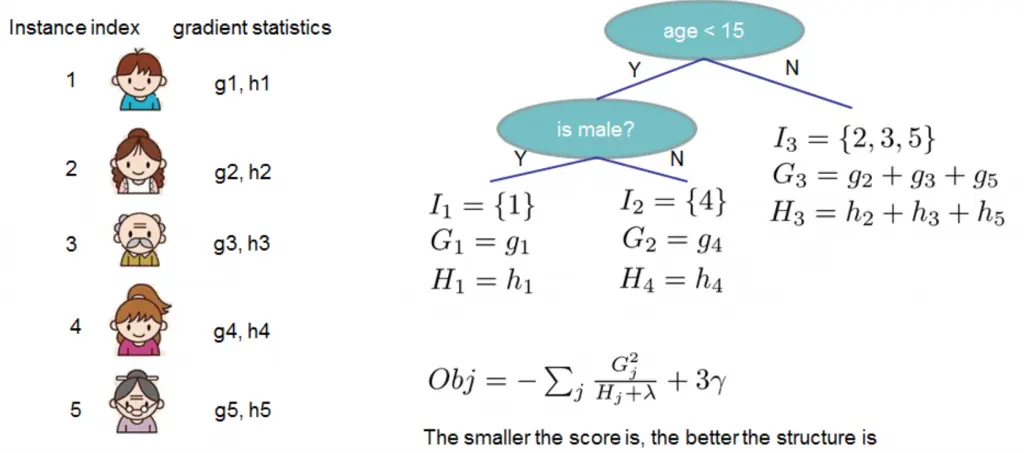
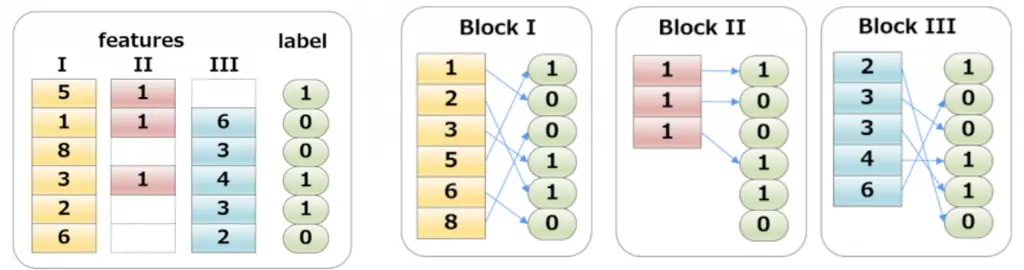
例子:
实际上我们无法枚举所有的树结构然后选择最优的树,xgboost 通过逐层优化的方式构建树模型。将一个叶子节点分裂为左右两个新的叶子节点带来的增益可以表示为:
上式就是 xgboost 的特征选择准则, Gain 越大代表分裂后带来的 loss 减少量越多,所以 Gain 越大越好.
策略:当 gain>0 或大于某个阈值时进行分裂,否则不分裂(相当于剪枝)
分裂点查找算法(split finding algorithm)
1. 贪心算法(exact greedy algorithm),即枚举所有特征的所有可能的划分点,取 gain 最大的方案
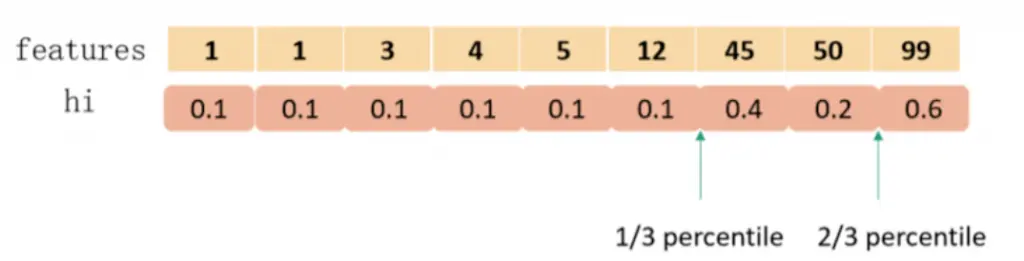
2. 加权分位点近似算法(approximate algorithm),即先对特征排序,以每个样本的二阶梯度值作为权重,基于权重按分位数来划分不同的候选分割点,取 gain 最大的方案(解决贪心算法在分布式环境或无法将所有数据加载到内存而导致的低效问题,大大减少了计算量)。
注意:此方法不是对样本进行均分(简单粗暴,但通常会导致分配不平衡),而是对样本的 loss 权重进行均分(相当于平衡各个分割区间的损失权重):
两种策略
global:全局分位点,只需要在每棵树初始化时对全局计算一次即可,但需要更精细,即分位点要更多(更多的桶 bucket)
local:局部分位点,每次分裂时都要重新计算一次,不需要太精细,即分位点比 global 少得多(更少的桶)
为什么以二阶梯度值作为权重?
已知目标函数:
可以改写成:
所以目标函数可以看成是以 (-gi)/hi 为 label 的带权平方误差损失,权重为 hi
如何防止过拟合?
1.目标函数引入正则项控制模型复杂度,提升泛化能力,正则项包含叶子节点数以及对叶子节点预测值进行 L2 正则化(平滑输出值)。
2.引入缩减因子(shrinkage),即模型更新方法为:
相当于减少每棵树的学习影响力,为后面的树提供更多的优化空间,η(eta)相当于模型的学习率,如果不引入缩减因子,则可能后面训练的树几乎不会对模型整体带来太大的影响,容易导致过拟合。
3.借鉴随机森林的做法,支持列采样(Column Subsampling),即特征采样,提升泛化能力同时减少计算量。
稀疏特征感知(处理缺失值和稀疏特征)
策略:将特征缺失的样本默认分到左节点,算一次增益得分,再默认分到右节点,算一次增益得分,哪边得分高就默认分到哪边。(减少了分裂点查找时间,提升训练效率)
特征粒度的并行训练
决策树学习最耗时的地方就是特征排序,XGBoost 通过 Column Block 结构(即对特征按列划分成不同的特征并对特征预先排序最终保存为特征块)
a) 特征已排序
b) 一个 block 包含多个特征值
c) 保存样本索引
d) 不保存缺失特征值
Column Block 可以在迭代学习中重复使用,同时也可以支持并行计算多个特征的分裂增益,大幅度提升训练效率。
预剪枝
当增益为负时不再分裂,但可能会错过将来某个时刻更高的增益
后剪枝
将树生长到最大深度,再递归剪去负增益的分支。
构建单棵树的时间复杂度
每层需要对于 n 个样本排序,复杂度为 O(n logn),有 d 个特征,深度为 K,所以总时间复杂度为:O(K d n logn)
为什么将损失函数进行泰勒展开?
不同的损失函数往往形式差异巨大,通过对损失函数进行二阶泰勒展开,使得最终的优化形式得到统一,那么对于不同的损失函数实际上使用完全一样的计算流程,只需要修改一阶导数和二阶导数的计算方式即可扩展到任意的损失函数。简单来说,泰勒展开主要是从算法实现的复用性和扩展性考虑。
为什么是二阶泰勒展开而不是一阶或者三阶?
二阶泰勒展开相比一阶更逼近原目标函数,并且收敛更快,更高阶的泰勒展开很可能会出现导数为 0 的情况。
算法流程整理
xgboost 与 传统 GBDT 的区别
- xgboost 基模型既支持 CART 模型也支持线性分类模型
- GBDT 只用到一阶导数信息进行优化(对损失函数求负梯度并进行拟合),XGBOOST 通过对损失函数进行二阶泰勒展开,得到构建第 t 棵树时损失函数的逼近表示,从而通过样本的一阶导数和二阶导数信息学习损失最小化的模型
- xgboost 支持列采样,提升泛化能力,减少运算量 【 泛化 】
- xgboost 引入了正则项,同时对叶子个数和权重进行惩罚,具有更好的泛化能力 【 泛化 】(传统 GBDT 只对叶子个数进行惩罚)
- xgboost 支持特征粒度的并行训练 【 加速 】
- xgboost 通过加权分位点近似算法查找分裂点,大幅度提升训练效率 【 加速 】
- 基于稀疏特征感知算法,xgboost 能高效处理缺失值和稀疏特征 【 加速 】
缺点
超参数多,调参困难