关于递归神经网络的理论介绍推荐阅读这篇非常经典的文章 → Understanding LSTM Networks
本文为总结笔记
一、RNN vs LSTM
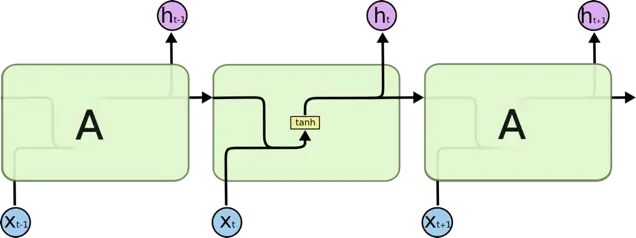
RNN 逻辑结构图
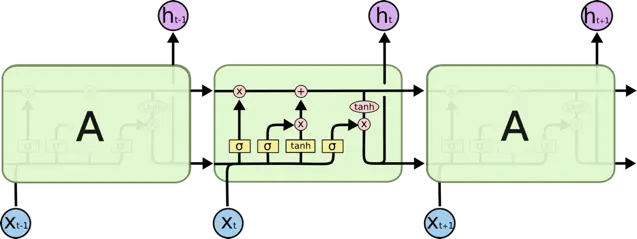
LSTM 逻辑结构图
LSTM 是 RNN 的变体,它们的原理几乎一样,唯一的不同是 output 即 hidden state 的计算逻辑不同
RNN 如何计算某个时刻 t 的 output ?
h_t = tanh(W*[h_{t-1}, x_t]+b)LSTM 如何计算某个时刻 t 的 output ?
遗忘门(Forget Gate): 控制遗忘哪些记忆(Cell state)
f_t = sigmoid(W_f*[h_{t-1}, x_t] + b_f)新信息:候选记忆信息
{C}^{*} = tanh(W_c*[h_{t-1}, x_t]+b_c)输入门(Input Gate):控制加入哪些新信息到记忆中
i_t = sigmoid(W_i*[h_{t-1}, x_t] + b_i)新记忆:遗忘部分旧记忆,加入部分新记忆信息,得到最新的cell state
C_t = f_t*C_{t-1} + i_t*{C}^{*}输出门(Output Gate):控制当前最新记忆的对应输出值
o_t = sigmoid(W_o*[h_{t-1}, x_t] + b_o)输出值:最终的 hidden state
h_t = o_t*tanh(C_t)当 Forget Gate=0, Input Gate=1, Output Gate=1 时 LSTM 与 RNN 等价
LSTM 为什么优于 RNN ?
RNN 通过叠乘的方式进行状态更新,当 sequence 比较长时容易出现梯度消失/爆炸的情况,主要原因是反向传播的连乘效应,而 LSTM 是通过门控制的叠加方式来更新状态(C_t的计算公式),所以可以有效防止梯度问题,当然对于超长的 sequence,LSTM 依然会有梯度消失或者爆炸的可能。
二、RNN/LSTM 中的 num_units 是啥意思 ?
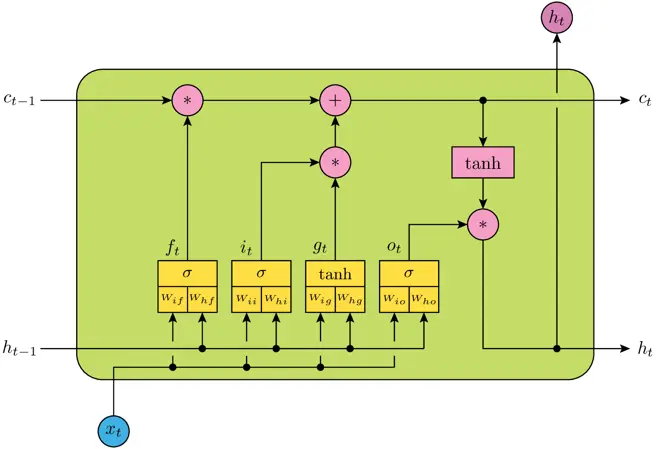
num_units 相当于神经网络的隐层神经元的个数,例如上图表示一个 LSTM Cell,包含四个神经网络层,即黄色方框部分,num_units 就是每个神经网络结构的隐层神经元个数(全连接单元数),它实际上也是 LSTM 输出向量的维度数,所以 h_t 为 num_units 维向量。
三、如何计算 Keras 的 LSTM layer 的参数个数?
假设 LSTM(num_units = 150),输入维度 input_dims = 100,那么共需要训练的参数个数为:
(num\_units + input\_dims + 1) * num\_units * 4 = 150600说明:
1. num_units + input_dims 是因为上层输出需要首先与输入进行一次concat,即 [h_t-1, x_t],
2. + 1 是因为 bias
3. * 4 是因为共有4个神经网络层(黄色方框)
4. 为什么不需要乘以 time_steps 即 number of cell ?
因为递归神经网络的每个 cell 实际上只是在不同时态下的状态,所以不同 cell 共用同一套权重,文章开头的结构图只是为了理解方便而将递归过程展开,实际上任何时候都只存在一个 cell !!
四、为什么 LSTM 要用 sigmoid 作为门控激活函数 ?
因为sigmoid的输出在0~1之间,可以很好地控制信息的删除和保留。
五、为什么 LSTM 的输入和输出值不用 sigmoid 而用 tanh 作为激活函数 ?
LSTM 内部维护了一个状态向量,其值应该可以增加或者减少,而 sigmoid 的输出为非负数,所以状态信息只能增加,显然不合适,相反,tanh 的输出范围包含了正负数,因此可以满足状态的增减。