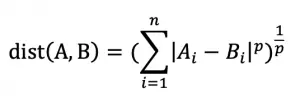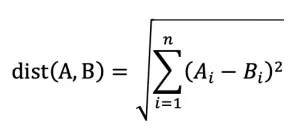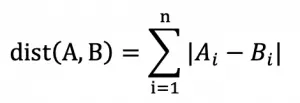KNN是一种用于分类和回归的监督学习算法,它无需对假设函数进行参数估计,因此它是一种非参数方法,KNN也是一种惰性学习(lazy learning)的算法,因为它与其它需要通过拟合数据来训练模型的算法不同,KNN算法没有训练环节!
KNN算法主要涉及三个因素
训练样本、距离(相似度)度量方式、k值选择。
预测基本步骤
- 计算当前样本与所有训练样本的距离。
- 取距离最近的K个样本作为邻居集合。
- 对于分类任务:邻居集合中出现次数最多的分类则为预测分类。
- 对于回归任务:计算邻居集合的平均数作为回归预测值。
备注:可以根据距离的倒数作为权重,计算加权平均数或加权次数,再进行排序。即距离越近的邻居有更高的权重,这种方法有助于降低样本不平衡的影响。
常用距离度量(连续特征)
明可夫斯基距离
欧几里德距离(p=2)
备注:维度越高,欧式距离的区分能力越弱, 即维度咀咒。
曼哈顿距离(p=1)
关于k值
- k值设置过小,容易受噪音数据影响,模型变得复杂,存在过拟合风险
- k值设置过大,容易受其他类别过多的影响,模型变得简单,存在欠拟合风险。(极端情况:k=样本数,那么样本数最多的类别是唯一的预测结果)
- 更大的k值有助于降低对噪音的敏感度,但同时也增加了计算复杂度。
- 可以通过交叉验证(Cross-Validation)选合适的k值
如何处理离散特征
- 将离散特征转化为数值特征(你需要知道特征之间的量化关系)
- 将离散特征用独热编码表示
- 自定义距离计算函数
查找k近邻的优化方式
- KD-Tree(需要大量内存)
- Ball-Tree(需要大量内存)
- 最近质心算法(即将每个类别的各特征平均数作为代表该类别的质心样本特征)
优点
- 算法简单。
- 不需要训练。
- 可用于非线性分类。
- 可用于多分类问题。
缺点
- 空间、时间复杂度高,不适合处理大规模训练集。
- 容易受无关特征影响。
- 不适合处理高纬特征。
- 当样本不平衡,对稀有类别的预测准确率较低。