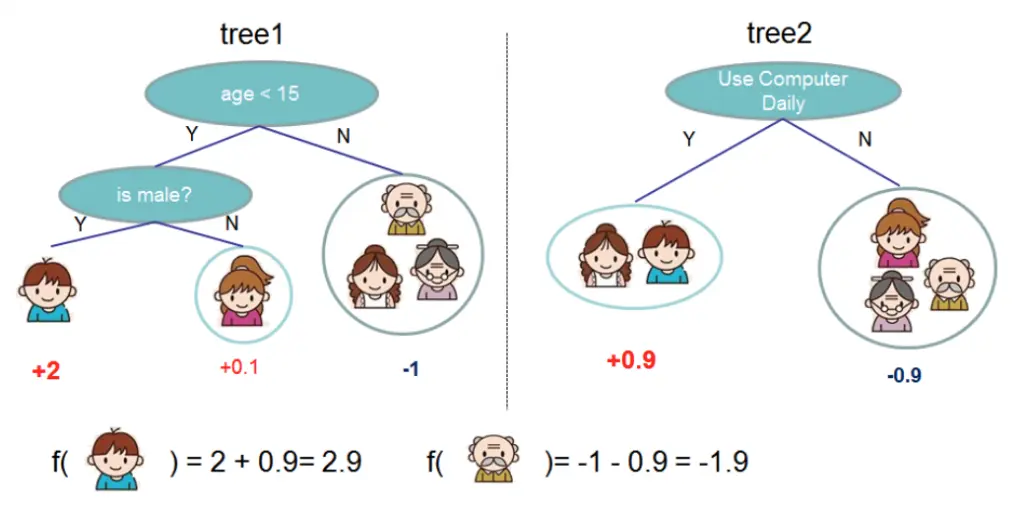
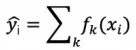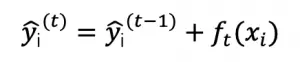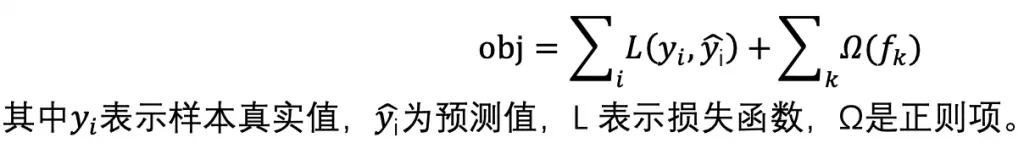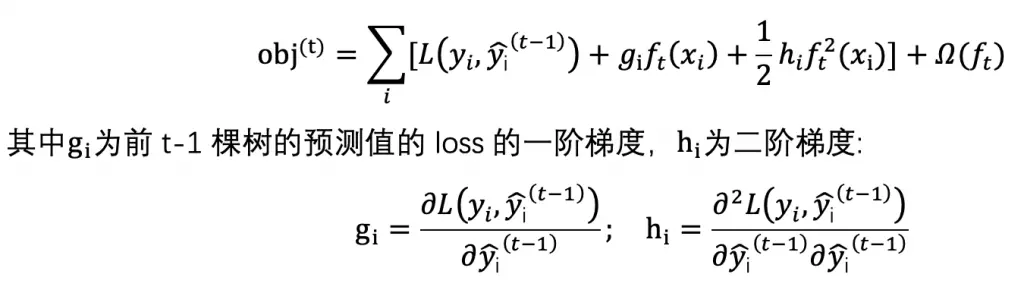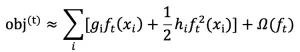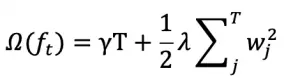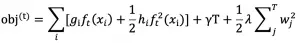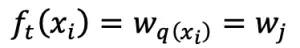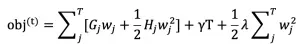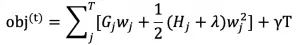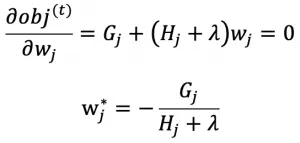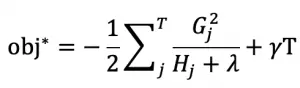xgboost 是对传统 GBDT 算法的一种改进实现,主要包括损失函数 、 正则化 、 分裂点查找优化 、 稀疏特征感知 、 并行化等方面.
原理推导
假设迭代训练 k 次,那么 xgboost 的模型函数可以表示为:
其中 k 表示决策树的数目,f 表示一棵 CART 树。那么,前 t 棵树的预测值可以表示为:
需要优化的目标函数为:
那么训练第 t 棵树的目标函数可表示为:
在前 t-1 棵树处进行二阶泰勒展开:
由于去除常数项 L 后不影响问题优化,因此目标函数化简为:
xgboost 定义正则项如下:
其中 T 为叶子数,wj 为第 j 个叶子节点的预测值(权重,prediction score)。目标函数为:
对于样本 xi ,在第 t 棵树的预测值表示为:
其中 q 表示树结构, q(xi) 表示样本 xi 在中被分到的叶子节点索引,wj 表示第 j 个叶子节点的预测值,因此原目标函数由样本表示形式(sample-wise)改写成树结构表示形式(structure-wise):
化简得:
其中 Gj 和 Hj 分别表示被分到第 j 个叶子节点的所有样本的 loss 的一阶(二阶)导数值之和,wj 表示第 j 个叶子节点的预测值(权重),T 表示叶子节点数。
对目标函数求关于 wj 的导数等于 0 即可得最优的预测值 wj^* 使得目标函数最小化:
将 wj^* 代入目标函数 obj^(t) 得 xgboost 的终极目标函数:
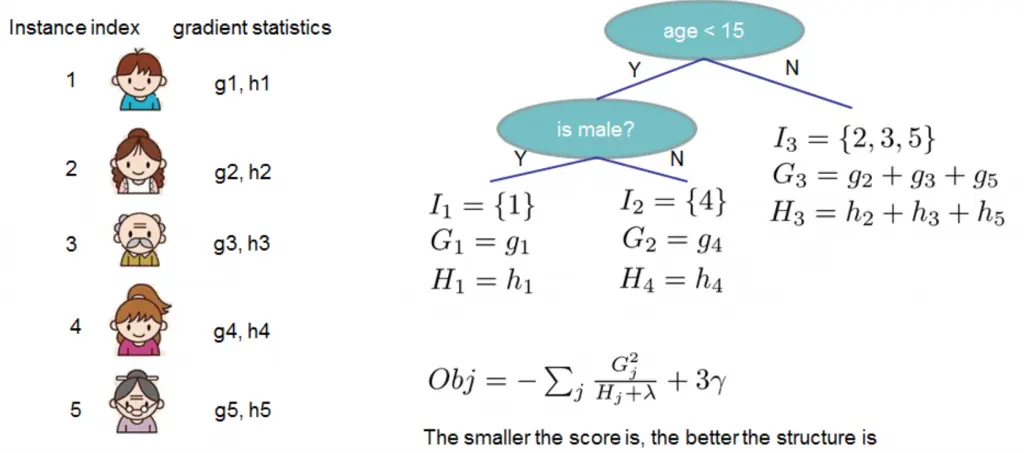
上式度量了一棵结构为 q(x) 的树的好坏,值越小越好!!!!
例子:
实际上我们无法枚举所有的树结构然后选择最优的树,xgboost 通过逐层优化的方式构建树模型。将一个叶子节点分裂为左右两个新的叶子节点带来的增益可以表示为:
上式就是 xgboost 的特征选择准则, Gain 越大代表分裂后带来的 loss 减少量越多,所以 Gain 越大越好.
策略:当 gain>0 或大于某个阈值时进行分裂,否则不分裂(相当于剪枝)