K-means算法是机器学习/数据挖掘领域广泛使用的聚类算法,它是一个无监督学习算法,即无需对样本进行事先标记。K-means算法通俗来说主要完成一件事:给定一个包含n个点的数据集,把该数据集划分到k个聚类中,使得各个聚类所包含的每个点到各自聚类中心的距离均小于与其他聚类中心的距离。
K-Means算法
(一)算法过程
1)确定要划分的聚类个数(K),从数据集D中任意选出K个点作为聚类中心
2)计算所有点到各个聚类中心的距离,把各个点归类到距离最近的那个聚类集中
3)计算第二步所产生的K个聚类集的中心,将该中心作为数据集D新的K个聚类中心
4)重复2)、3)直到中心点不再变化或迭代次数达到设定的最大迭代值或中心点的变化收敛于某个预定值
(二)算法分析
1)K-means算法的第一步需要确定任意的K个初始聚类中心,但实际上所谓的“任意”也有一定的原则,不恰当的选取初始中心点有时候会导致聚类结果并不理想,初始中心的选取也是K-means算法面对的困难之一,一般以彼此相距尽可能大的K个点作为初始中心点.
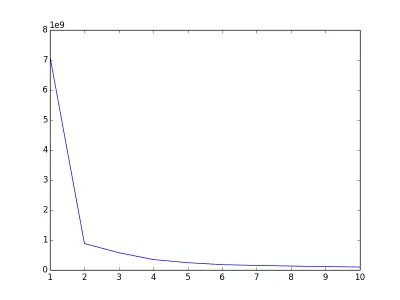
2)K-means算法还需要面对一个问题:到底这些数据应该分成多少个类型才合适?(即K=?)好的聚类结果应该是:各个聚类彼此间的数据特征差异很大,而聚类内的数据特征差异很小。可以用误差平方和(SSE)作为准则函数来评价,即聚类内各个点到聚类中心的距离的平方和。一般地,在合适的K范围内当SSE越少则聚类结果越好。之所以说“合适的K范围”,是因为当K太大,极端地当K等于数据集的元素个数时,此时每个点都是一个聚类,中心点就是自身,此时SSE=0,这显然不是一个理想的聚类结果。要选出合适的K值,一个常用的方法(The Elbow Method)是计算不同K值下的聚类结果的SSE,画出K-SSE的变化关系,选取发生抖动的那个点所在的值作为K值.(如下图,当k=2时发生了明显的抖动,对于该数据集我们认为K=2是个合适的选择)
3)K-means算法的第二步需要计算两点之间的距离,这个距离实际上是描述了两个点的相异度,评价的方法有很多种,例如:欧几里得距离、曼哈顿距离、闵可夫斯基距离公式等,距离计算方法的选取要结合实际的数据特征,并非所有情况都适合用欧几里得距离来衡量二者的相异度,例如对于一个曲面,空间上很接近的两个点,实际上在曲面上的距离可能非常远.
4)计算距离时需要考虑各个维度的特征值是否会对结果产生异常影响,例如:对于特征点(1,2,3,999)、(1,2,2,888)、(2,3,4,777)可以发现,第四维特征(即999、888、777)会直接主导了整个距离的结果,其他特征的特征值几乎对距离结果没有影响,这显然不符合距离的意义,这时候需要对特征值进行归一化处理.
(三)算法应用
参考 → K-Means聚类算法(实践篇)– 基于Spark Mlib的图像压缩案例

