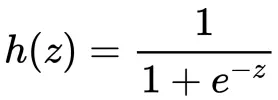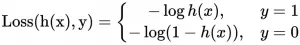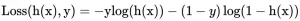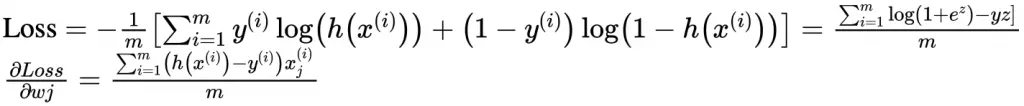逻辑回归是一种有监督的分类模型(离散型输出),它将线性函数的线性输出通过 Sigmoid 变换映射到 0~1 的范围,表示对应特征与对应输出的一种概率关系。逻辑回归本质上是一种广义线性模型,Sigmoid 只是非线性激活函数。

二分类
例子:根据医学指标特征来判断一个人是否患有癌症。
备注:输入数据服从高斯分布,输出数据服从伯努利分布(0-1分布)。
逻辑回归假设式(hypothesis)
其中z 是线性输出层,即 z = wX+b
Sigmoid 函数的导数可以用自身来表示:h(z)’=h(z)(1-h(z))
最大似然估计(MLE):
逻辑回归利用已知的试验结果,反推最有可能(最大概率)导致这样结果的参数值。
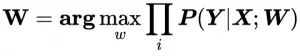
逻辑回归以对数似然损失作为损失函数(log loss)
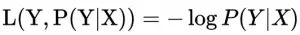
即在样本X的前提下,使得真实分类结果Y发生的概率最大时,损失最小。
备注:逻辑回归的平方损失函数为非凸函数,存在多个局部最优解,故不采用。
损失函数(Cost Function):
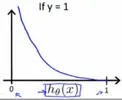
当 y=1 时,预测为正例的概率(即h(x))越大,模型的损失就越低,当h(x) = 1,即100%认为是正例时,模型损失最低,cost=0,表示完全预测正确.
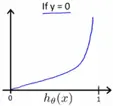
当 y=0 时,预测为正例的概率越大,模型的损失就越大,当h(x)=1,即100%认为是正例时,模型的损失趋向无穷大,表示完全预测错误。
合并损失函数多行式:
最终的损失函数形式为:
除了假设式h(x) 不同,偏导结果与线性回归完全一致。
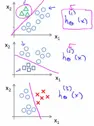
多分类 – 多个逻辑回归
One vs all (One vs rest):
将多分类问题看成多个独立的二分类问题,例如有A、B、C三个分类,那么训练以下三个分类器:
a) 将训练样本中A分类标记为1,其他标记为0,训练一个能识别是不是A的分类器
b) 将训练样本中B分类标记为1,其他标记为0,训练一个能识别是不是B的分类器
c) 将训练样本中C分类标记为1,其他标记为0,训练一个能识别是不是C的分类器
对于新的输入特征X,通过以上三个分类器进行预测,选择预测概率最大的那个分类器对应的分类作为预测的结果。