Author: FelixHo

FelixHo http://hejunhao.me Sometimes You Win, Sometimes You Learn.
日志

Softmax 回归

Softmax 回归是一种基于监督学习的分类算法，它是逻辑回归在多分类上的推广。它通过 Softmax 将线性输出层的结果进行归一化，分别表示不同分类的概率，并且所有概率之和为1。
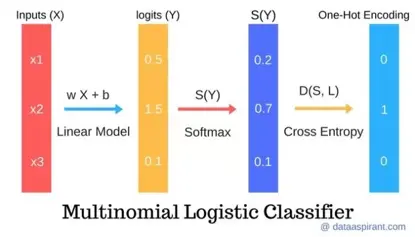
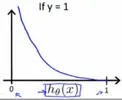
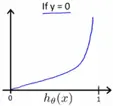
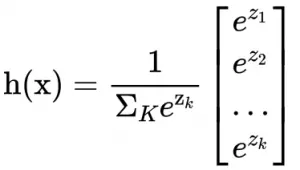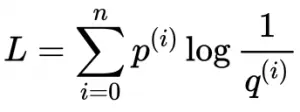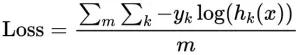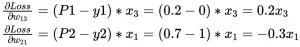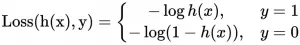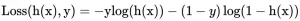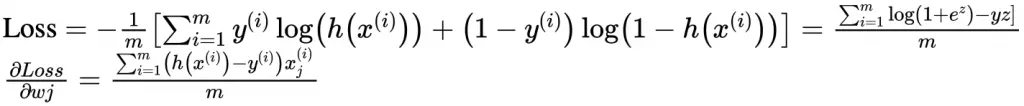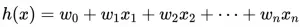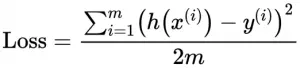Pasted

Softmax 回归假设式（hypothesis）：

其中 z 是线性输出层 即 z = wX + b

交叉熵（cross-entropy）:

其中p表示真实概率分布，q表示非真实概率分布;交叉熵可用于衡量真实标记的分布与预测标记的分布的差异程度。

Softmax 以交叉熵作为损失函数：

其中 m 表示样本数，k 表示分类数，如果某样本属于第 k 类，则 y_k =1，其余情况为0，h_k 表示某样本属于第 k 类的概率。

梯度计算:

解释：模型误差相对于第 k 类的第 j 个特征的权重的梯度 =（样本属于第 k 类的概率 – 该样本是否属于第k类（0或1）） x 样本第 j 个特征的值。

例如: 某样本（x1, x2, x3）标记为第2类

Pasted

什么时候用逻辑回归、什么时候用Softmax回归？

如果类别是互斥的，用Softmax，例如：香蕉、苹果、西瓜；
如果类别不互斥的，用多个逻辑回归，例如：黑白图片、户外图片、包含人的图片

转载请注明出处:

© http://hejunhao.me

日志

逻辑回归（Logistics Regression）

逻辑回归是一种有监督的分类模型(离散型输出)，它将线性函数的线性输出通过 Sigmoid 变换映射到 0~1 的范围，表示对应特征与对应输出的一种概率关系。逻辑回归本质上是一种广义线性模型，Sigmoid 只是非线性激活函数。
Pasted

二分类

例子：根据医学指标特征来判断一个人是否患有癌症。
备注：输入数据服从高斯分布，输出数据服从伯努利分布（0-1分布）。

逻辑回归假设式（hypothesis）

其中z 是线性输出层，即 z = wX+b
Sigmoid 函数的导数可以用自身来表示：h(z)’=h(z)(1-h(z))

最大似然估计(MLE)：

逻辑回归利用已知的试验结果，反推最有可能（最大概率）导致这样结果的参数值。
Pasted

逻辑回归以对数似然损失作为损失函数（log loss）

Pasted


即在样本X的前提下，使得真实分类结果Y发生的概率最大时，损失最小。
备注：逻辑回归的平方损失函数为非凸函数，存在多个局部最优解，故不采用。

损失函数（Cost Function）：

Pasted


Pasted

当 y=1 时，预测为正例的概率(即h(x))越大，模型的损失就越低，当h(x) = 1，即100%认为是正例时，模型损失最低，cost=0，表示完全预测正确.

Pasted

当 y=0 时，预测为正例的概率越大，模型的损失就越大，当h(x)=1,即100%认为是正例时，模型的损失趋向无穷大，表示完全预测错误。
合并损失函数多行式：

Pasted

最终的损失函数形式为：

除了假设式h(x) 不同，偏导结果与线性回归完全一致。

多分类 – 多个逻辑回归

One vs all (One vs rest):

将多分类问题看成多个独立的二分类问题，例如有A、B、C三个分类，那么训练以下三个分类器：
a) 将训练样本中A分类标记为1，其他标记为0，训练一个能识别是不是A的分类器
b) 将训练样本中B分类标记为1，其他标记为0，训练一个能识别是不是B的分类器
c) 将训练样本中C分类标记为1，其他标记为0，训练一个能识别是不是C的分类器

对于新的输入特征X，通过以上三个分类器进行预测，选择预测概率最大的那个分类器对应的分类作为预测的结果。

转载请注明出处:

© http://hejunhao.me

日志

线性回归（Linear Regression）

线性回归是一种监督学习算法，它是一种回归模型，它的目标是要找到训练样本的最佳拟合直线（回归线），从而使模型可以对新数据进行预测，它的预测结果属于连续型数值。
例如：根据面积、房间数、建筑年龄预测房子的售价。

线性回归模型假设式（hypothesis）:

Pasted

以均方误差（MSE）作为损失函数（cost function）:

Pasted Pasted

包含L2正则项情况:

Pasted



MSE用于度量预测值与真实值的偏离程度, 以梯度下降法最小化损失函数，从而使得模型学习到合适的权重参数。

权重更新过程：

Repeat until convergence {
Pasted


…
…
}
w_(j) 代表第j个权重, i 表示第 i 个样本，α 表示学习率

转载请注明出处:

© http://hejunhao.me

日志

K-Means聚类算法（实践篇）– 基于Spark Mlib的图像压缩案例

Spark Mlib 机器学习库集成了许多常用的机器学习算法，本文以K-Means算法为例结合图像压缩案例，简单介绍K-Means的应用。关于K-Means算法理论可以参考 → K-Means聚类算法（理论篇）

案例介绍

图像压缩

1）一张图由一系列像素组成，每个像素的颜色都由R、G、B值构成（不考虑Alpha），即R、G、B构成了颜色的三个基本特征，例如一个白色的像素点可以表示为（255,255,255）。

2）一张800×600的图片有480000个颜色数据，通过K-Means算法将这些颜色数据归类到K种颜色中，通过训练模型计算原始颜色对应的颜色分类，替换后生成新的图片。

Spark Mlib K-Means应用（Java + Python）

阅读全文 →

日志

K-Means聚类算法（理论篇）

K-means算法是机器学习/数据挖掘领域广泛使用的聚类算法，它是一个无监督学习算法，即无需对样本进行事先标记。K-means算法通俗来说主要完成一件事：给定一个包含n个点的数据集，把该数据集划分到k个聚类中，使得各个聚类所包含的每个点到各自聚类中心的距离均小于与其他聚类中心的距离。

K-Means算法

（一）算法过程

1）确定要划分的聚类个数（K），从数据集D中任意选出K个点作为聚类中心
2）计算所有点到各个聚类中心的距离，把各个点归类到距离最近的那个聚类集中
3）计算第二步所产生的K个聚类集的中心，将该中心作为数据集D新的K个聚类中心
4）重复2）、3）直到中心点不再变化或迭代次数达到设定的最大迭代值或中心点的变化收敛于某个预定值

（二）算法分析

阅读全文 →

日志

方差、标准差、均方误差、协方差的区别

简单介绍 方差、标准差、均方误差、协方差的基本概念以及计算公式，以区分它们的作用。

方差（Variance）

用来度量随机变量和其数学期望（即均值）之间的偏离程度

σ2=(x1−X¯)2+(x2−X¯)2...+(xn−X¯)2(n−1)=∑i=1n(xi−X¯)2(n−1)
σ^2 = \dfrac{(x_1 - \bar{X})^2 + (x_2 - \bar{X})^2 ... + (x_n - \bar{X})^2}{(n-1)} = \dfrac{\sum_{i=1}^n{(x_i - \bar{X})^2}}{(n-1)}


备注：n-1 原因是无偏估计

标准差（Standard Deviation）

又叫均方差 ， 反映一个数据集的离散程度（波动大小）.

标准差 = 方差的算术平方根

σ=(x1−X¯)2+(x2−X¯)2...+(xn−X¯)2(n−1)=∑i=1n(xi−X¯)2(n−1)
σ = \sqrt{\dfrac{(x_1 - \bar{X})^2 + (x_2 - \bar{X})^2 ... + (x_n - \bar{X})^2}{(n-1)}} =\sqrt{\dfrac{\sum_{i=1}^n{(x_i - \bar{X})^2}}{(n-1)}}

问：有了方差为何需要标准差？

答：标准差的量纲（单位）与数据集一致，更直观描述波动范围。

均方误差（Mean Squared Error）

用来度量预测值与真实值的偏离程度

y:预测值 ， Y:真实值

MSE=(y1−Y1)2+(y2−Y2)2...+(yn−Yn)2n=∑i=1n(yi−Yi)2n
MSE = \dfrac{(y_1 - Y_1)^2 + (y_2 - Y_2)^2 ... + (y_n - Y_n)^2}{n} = \dfrac{\sum_{i=1}^n{(y_i - Y_i)^2}}{n}

协方差 (Covariance)

两个变量有多大的“可能”朝一个方向改变？协方差用于度量这个“可能”的程度。如果两个变量的变化方向一致，那么协方差为正，反之为负。其中，变化指变量与它的数学期望的差值。

Cov(x,y)=(x1−X¯)(y1−Y¯)+(x2−X¯)(y2−Y¯)...+(xn−X¯)(yn−Y¯)(n−1)=∑i=1n(xi−X¯)(yi−Y¯)(n−1)
Cov(x,y) = \dfrac{(x_1 - \bar{X})(y_1 - \bar{Y}) + (x_2 - \bar{X})(y_2 - \bar{Y}) ... + (x_n - \bar{X})(y_n - \bar{Y})}{(n-1)}
         = \dfrac{\sum_{i=1}^n{(x_i - \bar{X})(y_i - \bar{Y})}}{(n-1)}

当 cov(x,y)>0 ，则 X 与 Y 正相关；
当 cov(x,y)<0 , 则 X 与 Y 负相关；
当 cov(x,y)=0 ，则 X 与 Y 不相关。

转载请注明出处:

© http://hejunhao.me

日志

Hadoop NameNode 高可用架构

NameNode是HDFS（hadoop分布式文件系统）的核心组件，在hadoop 1.x中NameNode存在SPOF（单点故障）问题，NameNode存储了HDFS的元数据信息，一旦NameNode宕机那么整个HDFS就无法访问，依赖HDFS的服务也会被波及（HBase、Hive…）同样无法访问，整个集群陷入瘫痪。NameNode的单点故障问题也使得Hadoop在1.x时代一直都只能用作离线存储和离线计算，无法满足对高可用要求很高的应用场景。Hadoop2.x针对NameNode的SPOF问题提出了高可用架构方案（HA），目前已经能在生产环境下应用。本文主要介绍该高可用架构的主备切换机制。

一、NameNode高可用架构

Hadoop NameNode高可用架构

Hadoop NameNode高可用架构

二、组件概述

Active NameNode 与 Standby NameNode

在NameNode的HA方案中有两个不同状态的NameNode，分别为活跃态（Active）和后备态（Standby），其中只有Active NameNode能对外提供服务，Standby NameNode会根据Active NameNode的状态变化，在必要时可切换成Active.

ZKFC

ZKFC即ZKFailoverController，是基于Zookeeper的故障转移控制器，它负责控制NameNode的主备切换，ZKFC会监测NameNode的健康状态，当发现Active NameNode出现异常时会通过Zookeeper进行一次新的选举，完成Active和Standby状态的切换

HealthMonitor

阅读全文 →

日志

Hadoop之YARN/MRv2

YARN又称为Mapreduce version 2（MRv2）是hadoop2.x的新架构，它将旧Hadoop Mapreduce框架中的JobTracker的资源管理和作业生命周期管理拆分成两个组件即ResourceManager(RM)和ApplicationMaster(AM)

一、为何需要MRv2？

mr1vsmr2

MRv1与MRv2对比

MRv1资源管理问题

  1. Hadoop1.0引入了“slot”的概念，每个slot代表了各个节点上的一份资源（CPU、内存等），MRv1把Map和Reduce的资源单独区分，即Map slot、Reduce slot，两个阶段的slot不能共享，这意味着资源的利用率大大降低
  2. 非MR应用不能分享资源，所以只能运行MR计算框架的应用
  3. 每个集群只有一个JobTracker,限制了集群的扩展，集群规模限制在4000个节点左右

MRv2资源管理方案

  1. 舍弃“slot”的概念，每个节点以“资源”（CPU、内存等）为单位分配给有需要的应用
  2. 支持运行MR应用和非MR应用
  3. JobTracker的大量功能被迁移到ApplicationMaster（AM），集群内可以存在多个AM（每个应用程序都拥有一个独立的AM），集群可以扩展到上万个节点

二、YARN架构

YARN_Architecture

YARN架构图(via Apache Hadoop)

资源管理器（ResourceManager，RM）

ResourceManager运行在主节点（Master）上，负责全局资源调度(分配/回收)，处理各个应用的资源请求，ResourceManager由调度器（Scheduler）和应用管理器（ApplicationsManager， AsM）组成

  • 调度器（Scheduler）
    调度器根据资源调度策略（例如Capacity Scheduler、Fair Scheduler），将包含适当资源（CPU、内存等）的资源容器（Container）分配给相应的节点，应用程序的各个任务均在容器内执行，且只能使用容器分配到的资源.调度器只负责资源调度，不关心应用的执行状态.
    阅读全文 →
日志

Hadoop之HDFS（NameNode、DataNode、SecondaryNameNode）

HDFS（hadoop分布式文件系统）是Hadoop的核心组成部分，HDFS采用master/slave架构，一个HDFS集群由一个NameNode（不考虑HA/Federation）和多个DataNode组成

hdfs架构

HDFS架构图（via Apache Hadoop）

一、NameNode

  • NameNode是HDFS的中心，也称作Master
  • NameNode只保存HDFS的元数据，负责管理HDFS的命名空间（namespace）和控制文件的访问操作
  • NameNode不保存任何实际的数据或数据集，真正的数据由DataNode负责存储
  • NameNode拥有HDFS内所有文件的数据块（blocks）列表及其位置，因而NameNode能通过这些数据块信息来重构对应的文件
  • NameNode是HDFS的核心，一旦NameNode挂了，整个集群将无法访问
  • NameNode具有单点故障问题（Hadoop2之后可以通过High Available方案解决）
  • NameNode需要配置相对较多的内存（相比DataNode而言），因为NameNode会把HDFS的命名空间和文件数据块映射（Blockmap）保存在内存中，这也意味着集群的横向扩展受到NameNode的限制，因为集群增长到一定的规模后NameNode需要的内存也会更大，另外由于所有的元数据操作都需要通过NameNode进行，这意味着集群的性能受到NameNode的限制（Hadoop2之后可以通过Federation方案解决）
  • NameNode有两个核心的数据结构，FsImage和EditsLog，FsImage是HDFS命名空间、文件数据块映射、文件属性等信息的镜像，EditsLog相当于一个日志文件，它记录了对HDFS元数据进行修改的所有事务操作，当NameNode启动时会首先合并FsImage和EditsLog，得到HDFS的最新状态然后写入FsImage镜像文件中，并使用一个新的EditsLog文件进行记录

SecondaryNameNode

“SecondaryNamenode”这个名字具有误导性，它不能和DataNode交互，更不能替代NameNode，相反它是用来弥补NameNode的一些缺点，由于NameNode启动时会合并FsImage和EditsLog，但随着集群的运行时间变长，EditsLog会变得非常庞大，这意味着下一次启动需要花很长的时间来进行合并操作.

SecondaryNameNode负责解决以上的问题
阅读全文 →

日志

kafka集群部署

Kafka是一个分布式的，可分区的，支持冗余备份的日志服务，提供消息系统功能，它相当于一条插口式的高速数据总线，主要用于处理活跃的流式数据，能有效降低系统组网的复杂度，和编程复杂度。本文主要介绍如何部署Kafka集群。

Kafka集群依赖Zookeeper集群协调管理，所以部署Kafka集群之前我们需要先搭建好Zookeeper Cluster

集群环境

假设有以下集群节点
hadoop1（192.168.10.1）
hadoop2（192.168.10.2）
hadoop3（192.168.10.3）

Zookeeper集群搭建

1）下载Zookeeper

Zookeeper Download

2）安装

将安装包解压到集群各个节点的指定目录下（$ZK_HOME）

3）配置

在$ZK_HOME/conf/创建zoo.cfg配置文件

  1. #基本时间单位，控制心跳和超时的基准
  2. tickTime=2000
  3.  
  4. #允许 follower （相对于 leader 而言的“客户端”）连接并同步到 leader 的初始化连接时间.
  5. #它以 tickTime 的倍数来表示。当超过设置倍数的 tickTime 时间，则连接失败.
  6. initLimit=10
  7.  
  8. #leader 与 follower 之间发送消息，请求和应答时间长度.
  9. #如果 follower 在设置的时间内不能与leader 进行通信，那么此 follower 将被丢弃.
  10. syncLimit=5
  11.  
  12. #自动清理事务日志和快照的时间间隔（小时）
  13. autopurge.purgeInterval=24
  14.  
  15. #需要保留的快照文件数
  16. autopurge.snapRetainCount=30
  17.  
  18. #存储数据的位置
  19. dataDir=/hadoop/zookeeper
  20.  
  21. #监听客户端连接端口
  22. clientPort=2181
  23.  
  24. #指定集群的机器配置，配置格式为“server.id=host:port:port”，其中id必须唯一.
  25. #并且需要在各台机器的dataDir下创建一个myid的文件，在myid文件中输入对应机器的id值.
  26. #另外，第一个端口（ 2888 ）是follower机器连接到leader机器的端口，第二个端口（3888）是用来进行leader选举的端口.
  27. server.1=hadoop1:2888:3888
  28. server.2=hadoop2:2888:3888
  29. server.3=hadoop3:2888:3888

4）运行

在各个节点上启动zookeeper

  1. $ZK_HOME/bin/zkServer.sh start

观察zookeeper运行状态

  1. $ZK_HOME/bin/zkServer.sh status

Kafka集群搭建

阅读全文 →

第 3 页，共 6 页123456