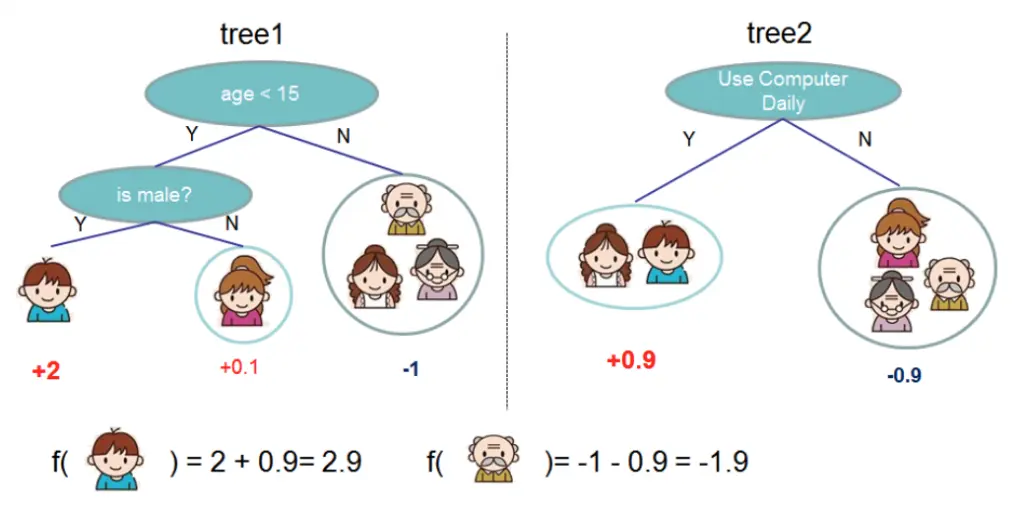
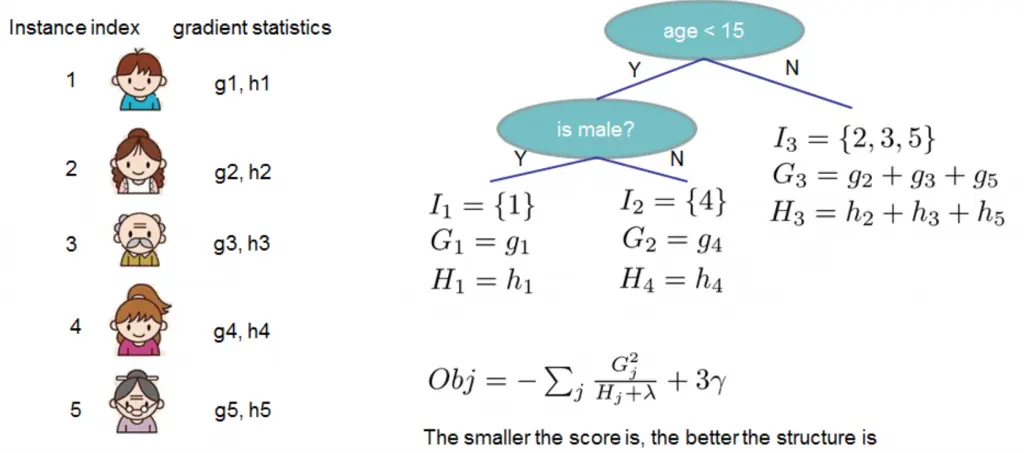
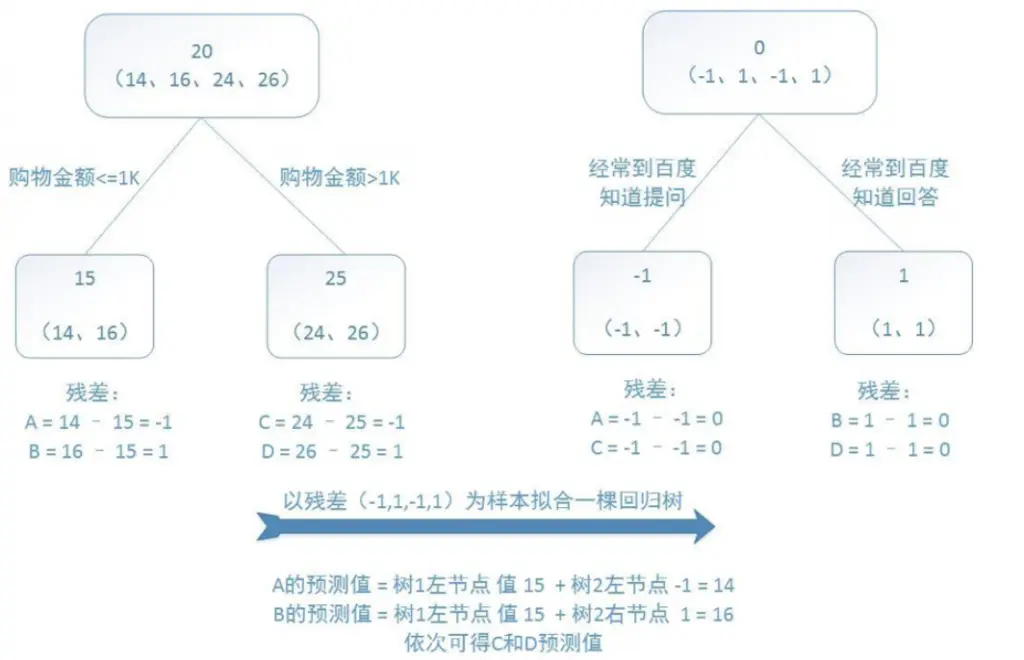
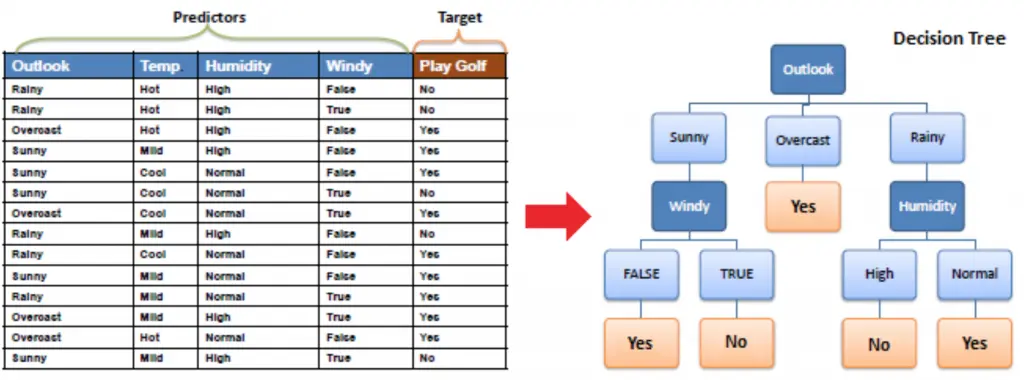
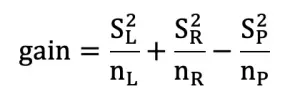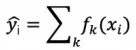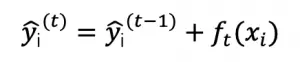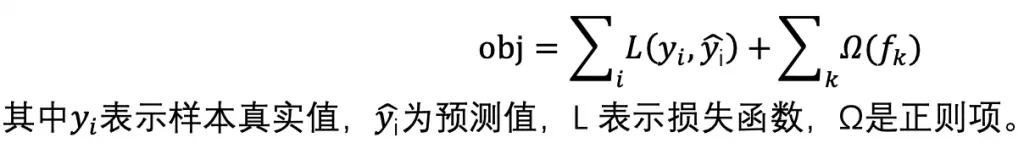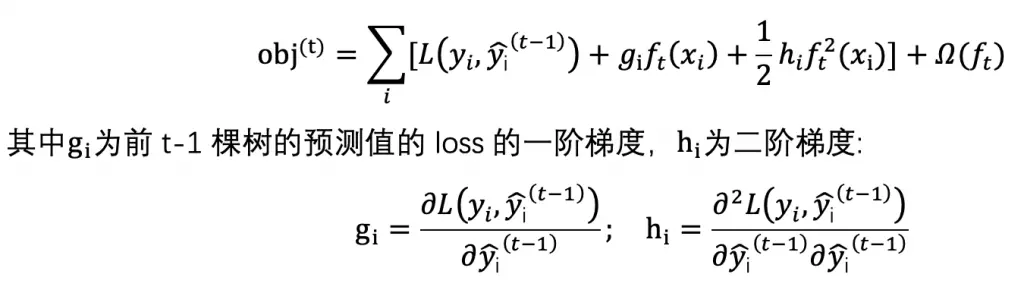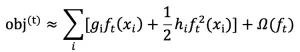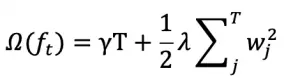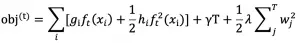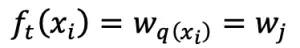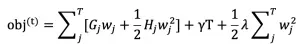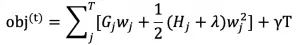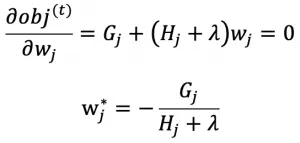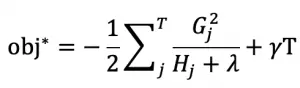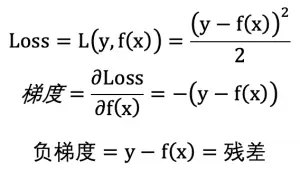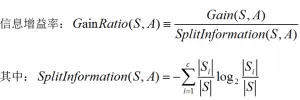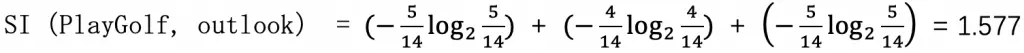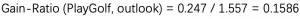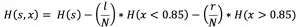LightGBM 是一种基于决策树算法的快速 、 分布式 、 高性能的 GBDT 框架,它是传统 GBDT 算法的一种改进实现,“Light”主要体现在三个方面,即更少的数据 、 更少的特征 、 更少的内存,分别通过 GOSS(单边梯度采样)、 EFB(互斥特征捆绑)和 Histogram(直方图算法)三项技术实现。
GOSS (Gradient-based One Side Sampling 单边梯度采样)
GOSS 是一种采样方法,在每次迭代前,先对样本进行采样,保留梯度变化最大的 a% 个样本,为了不改变样本分布,还需要从剩下的梯度变化较小的样本中随机采样 b% 个样本,并给予这 b% 个样本 (1-a)/b 的权重,这两部分样本为最终的训练样本。通过 GOSS 既保留了重要的样本,又在保持样本分布的同时大大减少了训练样本数,从而实现不影响模型准确性的同时大幅度提升训练效率。
GOSS 为什么以梯度作为样本权重?
因为 GBDT 对 loss 的负梯度进行拟合,所以样本误差越大,梯度的绝对值越大,证明模型对该样本的学习还不足够,相反如果越小证明模型对该样本的学习已经很充分,所以梯度的绝对值越大,样本重要性越高。(梯度是某一点最陡峭的地方,梯度大小形容它有多陡峭)
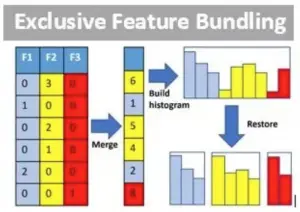
EFB(Exclusive Feature Bundling 互斥特征捆绑)
对于具有高维稀疏特征的数据,很多特征是互斥的(即多个特征之间最多只有一个特征的取值为非 0),EFB 通过捆绑多个互斥特征形成一个“大特征”,从而大大减少特征的数量,相当于是一种降维的方法。
例如,特征 A 的取值为 0~10,特征 B 的取值为 0~20,A、B 为互斥特征,那么捆绑 A/B 形成特征 C,特征 C 的取值为 0~30,所以 B=5 与 C=15 是等价的。
构造特征直方图是训练 GBDT 的主要时间消耗,而构造特征直方图的时间取决于需要遍历的特征数量,通过 EFB 方法可以减少特征的数量从而加快训练的效率。
备注:找出最优的 bundle 组合数是一个 NP 问题,LightGBM 通过贪心近似算法解决。即转化为图着色问题,图中的点为特征,非互斥的特征用一条边连接,边的权重为相连特征的总冲突值,那么着色相同的点即为互斥点(特征)
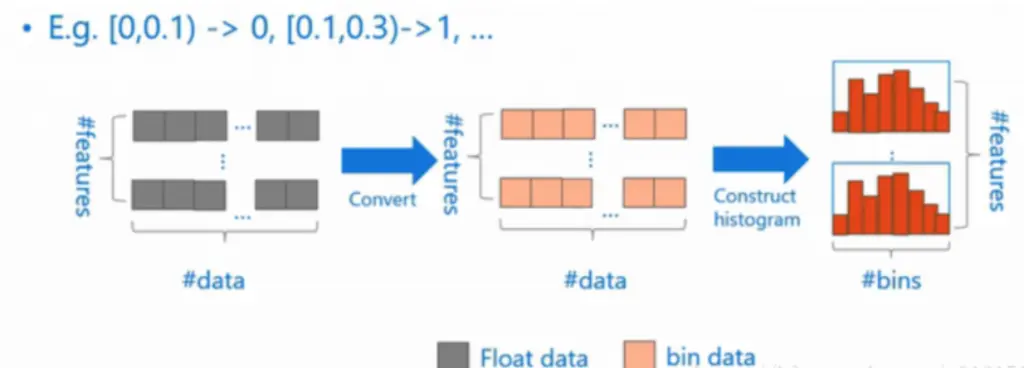
直方图优化算法(Histogram)
LightGBM 基于直方图算法优化查找最佳分割点的效率,在训练前首先通过直方图算法将连续特征离散化,相当于对特征的值进行分段划分,形成 k 个 bins(即 k 个离散值),构造一个宽度为 k 的直方图,在遍历数据时,根据离散值在对应 bin 上累积统计量(即梯度 g,样本数 n)。通过累积的统计量计算分裂增益,通过遍历所有 bin 寻找该特征的最佳分割点。
流程总结
- 特征离散化,得 k 个 bins,形成宽度为 k 的直方图
- 遍历数据,根据离散值在对应 bin 上累积统计量(g、n)
- 遍历 bins,通过累积统计量计算不同划分的分裂增益,求得最佳分割点
增益计算公式:
其中 S 为梯度之和,n 为样本数,L/R/P 表示左 / 右 / 父节点
优点:
- 传统的 pre-sorted 算法(例如 XGBoost 的 exact greedy 算法)在计算某个特征的分裂增益时需要遍历所有的特征值的划分情况,而直方图算法只需要遍历 k 个 bins 的划分情况,时间复杂度从 O(#data * #features) 降到 O(#bins * #features),大大减少了计算量。
- 传统的 pre-sorted 算法需要对特征预排序,而直方图算法没有排序要求,进一步提升了效率。
- 直方图算法可以通过做差加速,即只需要知道父节点的直方图,和任一子节点的直方图,即可通过做差得到其兄弟节点的直方图,效率提升一倍。
- 由于直方图算法没有排序要求,因此不用额外存储排序索引,另外离散化后的特征值可以用更小的数据类型表示(例如 256 个 bin 则只需要用 8 位整型表示,即从通常的 4 字节降到 1 字节),以上两点都可以大大减少内存的占用。
分析:直方图算法主要围绕着训练更快 、 内存占用更少两个方面进行优化,虽然它找到的并不是最精确的分割点,但对最终的模型精度影响并不大,而且较粗的分割点本身也有正则化的效果,有时甚至会有更好的精度。另外,对于 bosting 框架而言,决策树本身是弱模型,单棵树的误差变化稍大,对最终的结果没有太大的影响。