机器学习

日志

NLP 关键词提取算法之 TextRank

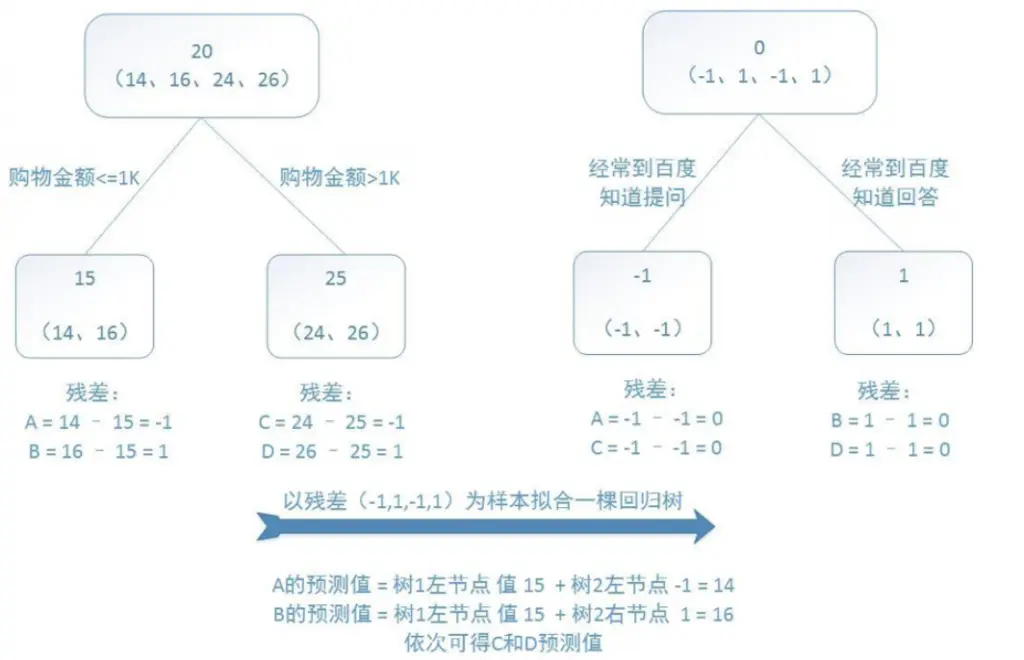
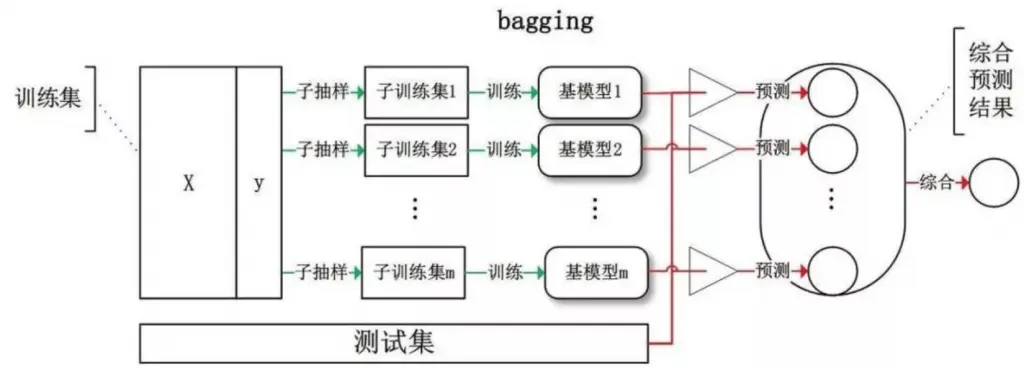
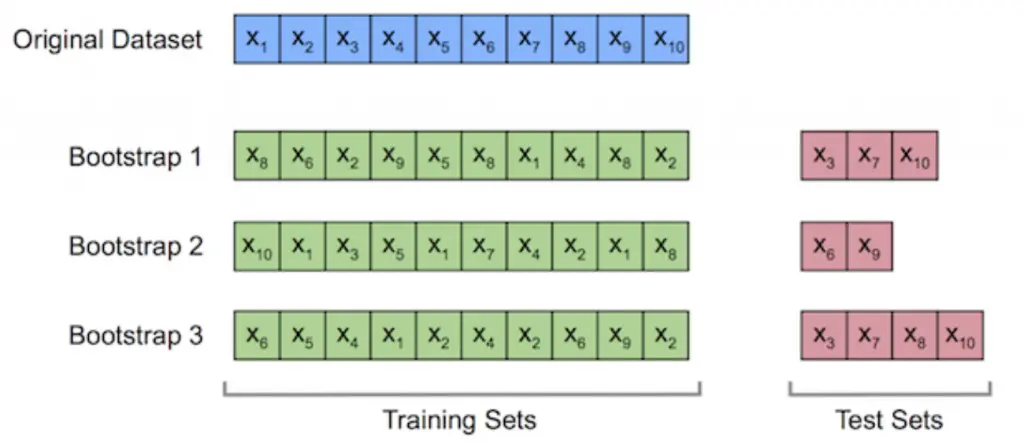
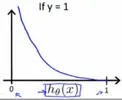
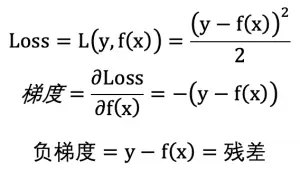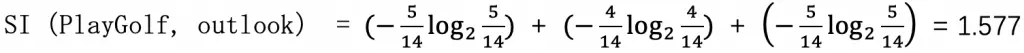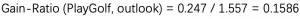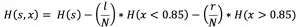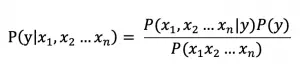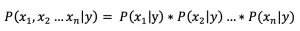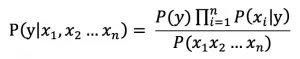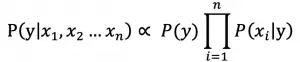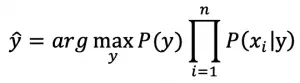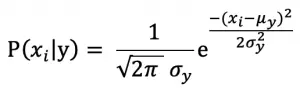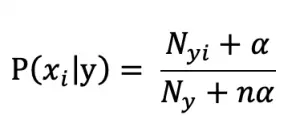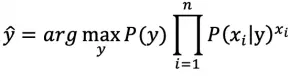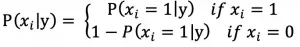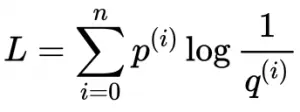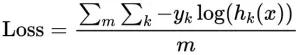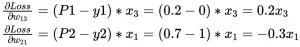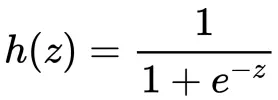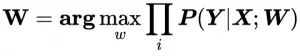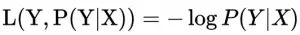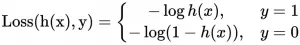对文本提取关键词，除了经典的 TF-IDF 算法，还有另一种常用的算法 — TextRank

TextRank 介绍

TextRank 是一种基于图的排序算法，它的基本思想来自于著名的 Google PageRank.

PageRank via @Wikipedia

图：PageRank via @Wikipedia

PageRank 的基本思想

  • 一个网页的入链越多，它就越重要。
  • 如果一个网页被越重要的网页所指向，它也越重要。

TextRank 算法简释

下图是通过 TextRank 进行关键词提取的一个简单例子
例子

图：通过 TextRank 提取文本关键词

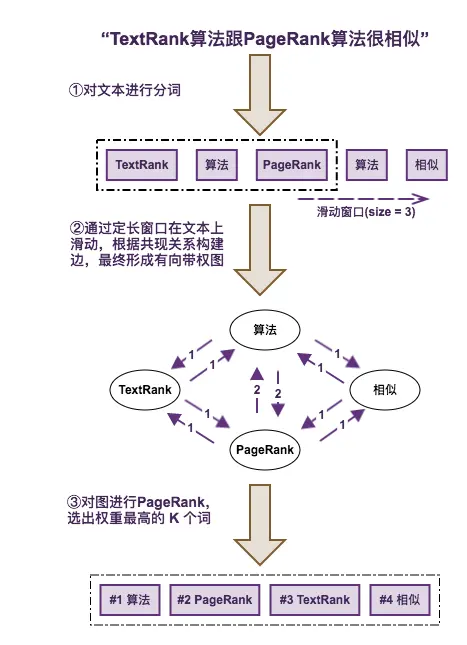
通过 TextRank 进行关键词提取的主要步骤

  1. 对文本进行分词，并去掉停用词以及非目标词性词汇。
  2. 通过一个固定长度的滑动窗口在分词文本上滑动，每个窗口内的词根据共现关系构建一条边，最终形成一个图。
  3. 对图进行 PageRank，实际上就是投票和迭代的过程。
  4. 选出权重最高的 TopK 个词。

算法总结

  • TextRank 算法一定程度上考虑了文本中词与词之间的关系，也就是文本结构，在实际应用中它的效果一般会比 TF-IDF 好，当然它的计算复杂度也比 TF-IDF 高得多。
  • TextRank 算法更擅长处理长文本，对短文本的效果并不理想，主要因为短文本的词汇信息较弱，构建的图并不理想。
  • TextRank 算法仍然倾向于选择出现较为频繁的词作为关键词。
转载请注明出处:

© http://hejunhao.me

日志

NLP 关键词提取算法之 TF-IDF

TF-IDF 是处理 NLP 问题时经常使用的经典算法，常用于对文本进行关键词的提取。

TF-IDF 介绍

计算公式

TF-IDF 的计算非常简单


TF-IDF = TF(\text{文章词频}) * IDF(\text{逆文档频率})

概念解释

TF: 指某个词在一段文本中出现的词频


TF = \dfrac{\text{某个词在文章中出现的次数}}{\text{文章总词数}}

IDF: 指某个词在所有文本（对应语境所在的训练语料，例如：科学领域、体育领域）中的区分度，它认为越少出现的词区分度越高，相应的 IDF 值也越高。


IDF = \log\dfrac{(\text{训练语料的总文档数+1})}{(\text{出现该词的文档数+1})}

分母 “+1” 是为了防止分母为零，同时相应地分子 “+1” 以防止 IDF 为负数。

算法总结

经验

从计算公式可知，TF-IDF 的准确性非常依赖 IDF 模型的质量。同一个词在不同领域对应的区分度（IDF）也不同甚至差别巨大，例如 “冠军” 在体育领域的语料中出现的次数远远大于在政治领域的语料中所出现的次数，这意味着在后者的语境下，“冠军” 这个词的区分度更高，IDF 值更大。要提升 TF-IDF 的算法效果一般需要根据业务场合单独训练特定领域的 IDF 模型。

评价

  • TF-IDF 计算复杂度低，适合对效率优先的场景。
  • 由于它只依赖关键词的统计特征进行排序，有时候效果并不理想，比如有时候文本的关键要素不一定是频繁出现的元素。
  • 另外它也缺乏对文本结构的考虑。
转载请注明出处:

© http://hejunhao.me

日志

GBDT

GBDT 是一种以梯度提升（Gradient Boosting ）作为训练策略，以回归决策树（Decision Tree，通常是 CART 回归树）作为弱模型的集成学习算法。其中梯度提升指每次迭代中通过拟合当前模型损失函数的负梯度（伪残差）来学习新的模型 ，从而通过结合新的模型使得模型损失进一步降低，而最终将多个模型结合的过程就是损失函数最小化的过程。

GBDT 分为 G、B、DT 三个部分

DT:即 decision tree 决策树，准确来说是回归树
B:即 boosting,指串行集成的模型结构
G:gradient,它通过拟合当前模型的损失函数的负梯度（残差）来学习新的模型

当以最小平方损失（LeastSquaresError）作为损失函数，此时损失函数的负梯度与残差（真实值 – 预测值）等价：

因此，每个弱模型的生成都是对前面所有模型的累加结果的残差的修正。

GBDT 原始论文算法描述

阅读全文 →

日志

集成学习（ensemble learning）

通过结合多个模型来完成学习任务，生成更强大的模型，相比单一模型，集成学习往往具有更好的泛化能力。根据结合的模型的类型是否相同（是否由相同算法生成），可以分为同质和异质。

根据结合方式的不同，集成学习可以分为两大类
模型之间不存在强依赖关系，可以并行训练，例如：Bagging、Random Forest
模型之间存在强依赖关系，必须串行化训练，例如：AdaBoost

Bagging(并行集成)

  1. 为了保证每个基模型的差异（集成学习的关键，样本差异可以使得模型关注不同角度），每个模型的训练集通过自助采样(.632 Bootstrap 采样)的方式生成 。
    自助采样：等概率 、 有放回地从训练集中抽取 n 个样本作为训练集（相同样本可能出现多次），其余没有被抽到的样本作为测试集，原始训练集的 63.2% 的样本会出现在训练集中。
  1. 输出预测方式：投票法（分类），平均法（回归）
  2. 优点：
    由于多个模型可以并行训练，所以训练比较高效 ；
    结合多个模型的预测能力，能有效提升泛化能力（即更低的方差 low variance）

Bias：训练样本准确率（更复杂的模型）
Variance：测试样本的准确率（泛化能力,更简单的模型）

Boosting(串行集成)

  1. 从初始训练集学习一个基模型。
  2. 根据上一个基模型的表现调整训练样本的分布（增加误分样本的权重，降低正确分类样本的权重）。
  3. 基于新的样本分布初始化新的训练集（误分样本更被重视）训练新的基模型。
  4. 重复以上步骤直到生成 T 个模型，通过加权线性结合所有基模型并进行预测。
  5. 偏向降低模型偏差（bias）

AdaBoost

阅读全文 →

日志

决策树 (Decision Tree)

决策树是一种非参数的监督学习算法，用于分类和回归任务，具有很强的解释性。决策树算法通过学习训练样本的特征，构建树状决策模型，最终生成一系列决策规则用于预测。

ID3 ( 信息增益, 分类算法，只支持类别特征，多叉树结构 )

特征选择准则

信息熵 ： 随机变量 Y 的不确定程度

条件熵 ： 在某一条件 X 的限制下，随机变量 Y 的不确定程度

信息增益 （Information Gain）： 条件 X 减少随机变量 Y 的不确定性的程度

信息增益 = 信息熵 – 条件熵

说明 ： 是否 PlayGolf 这件事的不确定性为 0.940，如果知道 outlook 的话，那么这种不确定性会减少 0.247

ID3 决策树构建步骤

  1. 计算每个特征的信息增益
  2. 选择信息增益最大的特征作为决策树的节点，并根据其特征取值分裂出分支节点
  3. 如果分支节点的熵为 0（ 即该节点的分类决策完全一致 ），则该节点为叶子节点，如果熵大于 0，则继续分裂。
  4. 重复 1-3 的步骤，直到所有特征的信息增益小于阈值或没有特征可用为止。

ID3 算法只有树的生成，所以该算法产生的树容易过拟合。

C4.5 ( 信息增益率，分类算法，支持类别特征 + 连续特征，多叉树结构 )

C4.5 是对 ID3 的一种改进，ID3 使用信息增益作为特征选择准则，但信息增益有一个缺点，它偏向于选择特征取值种类多的特征，即特征取值种类多的特征信息增益往往比较大。例如，以身份证号码作为特征，由于每个样本的身份证号码都是唯一的，每个取值只有一个样本，一个分类，所以每个取值的条件熵为:

那么信息增益会被最大化，但这种特征显然不是合理的分裂节点，因为通过已知的身份证号码来预测未知用户显然是不可取的。

信息增益率 （Gain-Ratio）

c4.5 采用信息增益率作为特征选择的准则

例如 ：outlook 特征取值为 sunny（5 个 ）, overcast（4 个 ）, rainy（5 个 ），总样本数 14 个，则 outlook 这个特征的分裂信息为 ：

信息增益率为 ：

启发式特征选取

信息增益率偏向于选择特征取值种类数较少的特征 （ 某个 Si 趋向于 S 时，分裂信息接近 0，信息增益率会非常大 ），可以通过启发式策略，先选取信息增益大于平均值的特征，再从这些特征中选取信息增益率最大的特征作为分裂节点。

连续特征处理

处理连续特征首先需要对连续特征进行离散化处理，即设定一个阈值分割连续特征，使其成为二类特征，而关键点在于如何选择合适的分割阈值。
1. 对连续特征的所有取值进行排序
2. 分别选取每两个取值之间的中点作为候选分割点。如果有 n 种取值，则有 n-1 个候选分割点
3. 计算不同分割方式的信息增益，信息增益最大的分割点作为最优分割点，并计算该分割方式下的信息增益率作为该特征的信息增益率。

例如:
连续特征 ：0.5, 1.2, 3.4, 5.4, 6.0
以 （0.5 + 1.2）/ 2 = 0.85 作为分割点，计算信息增益 ：

其中 l 是分割点左边的样本数，r 是分割点右边的样本数，N 是样本总数.
以 (1.2+3.4) / 2 = 2.3 作为分割点，计算信息增益 … 以此类推

CART（ 基尼指数，分类 、 回归算法，支持类别特征和连续特征，二叉树结构 ）

阅读全文 →

日志

KNN（K-Nearest Neighbors）

KNN是一种用于分类和回归的监督学习算法，它无需对假设函数进行参数估计，因此它是一种非参数方法，KNN也是一种惰性学习（lazy learning）的算法，因为它与其它需要通过拟合数据来训练模型的算法不同，KNN算法没有训练环节！

KNN算法主要涉及三个因素

训练样本、距离（相似度）度量方式、k值选择。

预测基本步骤

  1. 计算当前样本与所有训练样本的距离。
  2. 取距离最近的K个样本作为邻居集合。
  3. 对于分类任务：邻居集合中出现次数最多的分类则为预测分类。
  4. 对于回归任务：计算邻居集合的平均数作为回归预测值。
    备注：可以根据距离的倒数作为权重，计算加权平均数或加权次数，再进行排序。即距离越近的邻居有更高的权重，这种方法有助于降低样本不平衡的影响。

常用距离度量（连续特征）

阅读全文 →

日志

朴素贝叶斯（Naive Bayes）

朴素贝叶斯算法是一种基于贝叶斯理论的监督学习算法

对于一个含有n个特征（x1，x2 … xn）的样本，由贝叶斯理论可知它属于类y的概率为：

朴素贝叶斯算法假设特征之间是独立的，所以有:

因此有：

由于 P(x1 x2…xn ) 对所有类别是相同的，可以省略，即：

分别计算各个类别的概率，概率最大的类别则为最终的分类（最大后验概率），因此朴素贝叶斯算法最终表示为：

备注：P(y) 表示训练样本中类y的样本占比（先验概率）。

常见模型

朴素贝叶斯模型主要有三类常见的变形，即高斯模型、多项式模型以及伯努利模型。它们最大的不同在于对条件概率 P(x_i│y) 的计算差异，即对先验分布的假设不同。

高斯朴素贝叶斯模型（Gaussian Naive Bayes）：

当特征是连续变量（身高、年龄）时，可以假设特征符合高斯分布，则

其中 μ_y 为类y样本中特征 x_i 的平均数，σ_y 为 y 类样本中特征 x_i 的标准差。
训练高斯模型实质是就是计算每个类别对应于特征的均值和标准差，例如：
{0:[(mean1, std1), (mean2, std2)], 1:[(mean1, std1), (mean2, std2)]}

多项式朴素贝叶斯（Multinomial Naive Bayes）：

多项式模型可用于处理离散特征，例如：文本分类问题，特征 x_i 表示某个词在样本中出现的次数（当然用TF-IDF表示也可以）。条件概率计算公式为：

N_yi 表示类 y 的所有样本中特征 x_i 的特征值之和；
N_y 表示类 y 的所有样本中全部特征的特征值之和；
α 表示平滑值（α∈[0-1]），主要为了防止训练样本中某个特征没出现而导致 N_yi=0，从而导致条件概率 P(x_i│y)=0 的情况，如果不加入平滑值，则计算联合概率时由于某一项为 0 导致后验概率为 0 的异常情况出现。
n 表示特征总数。
多项式模型的预测公式为（即需要考虑出现次数的权重）：

伯努利朴素贝叶斯（Bernoulli Naive Bayes）:

伯努利模型的特征为布尔型，即只有1或者0两个取值，例如：在文本分类问题中，表示某个词是否出现在样本中。与多项式模型不同的是，多项式模型只考虑存在的特征，不存在的特征直接忽略条件概率的计算，而伯努利模型考虑的是全局特征，即使某个特征不存在，也会考虑不存在的可能性，条件概率计算公式为：

合并两式得：

伯努利模型适合处理短文本分类问题，因为相比计算某个词出现的次数，短文本往往对某个词是否出现更敏感。

技巧

阅读全文 →

日志

SVM（Support Vector Machine）

SVM是一种二元分类模型（当然它也可以处理回归问题），它通过训练样本寻找分隔两类样本的最优决策边界（超平面），使得两类样本距离决策边界的距离最远（例如H3）。其中距离决策边界最近的样本称为支持向量（即深色的苹果和香蕉），支持向量所在的与决策平面平行的平面称为支撑平面（虚线），支撑平面与决策平面的距离称为间隔（margin），SVM寻找最优决策边界实际上就是要最大化（最大可信度）两个支撑平面的间隔（决策平面位于两者的中间）。

SVM 模型根据数据集的差异可以分为三种类型：

  1. 线性可分 => 硬间隔最大化 => 线性可分SVM
  2. 线性不可分（有噪音）=> 软间隔最大化 => 线性 SVM（引入松弛变量和惩罚函数）
  3. 非线性可分 => 软间隔最大化 + 核函数 => 非线性 SVM

一、线性可分（硬间隔最大化）

图片 1

假设决策超平面为: W·X + b = 0
正类支撑平面为: W·X + b = γ
由对称关系可知负类支撑平面为: W·X + b = -γ
由于平面等比例缩放依然属于同一平面, 即 5W·X + 5b = 5 与 W·X + b = 1 是同一个平面
所以前面的假设可以更简洁地表示为（按γ等比例缩放）：
决策平面: W·X + b =0
正类的支撑平面: W·X + b = 1
负类的支撑平面: W·X + b = -1
要求满足以下规则：
Pasted

计算两个支撑平面的距离（margin）

由两平面距离公式可知，平面 W·X + b + 1 = 0 与平面 W·X + b -1 = 0的距离为：

所以要最大化margin相当于要最小化 ||w|| 即等价于：

最终的优化问题（目标函数）变成:

二、线性不可分（软间隔最大化）

当训练数据含有噪音数据时，如果进行硬间隔最大化可能会导致间隔过小甚至无法求解。

此时我们引入松弛变量（Slack Variable）ξ (epsilon ξ≥0) ，将原来的不等式约束变为：

松弛变量相当于为支撑平面提供了一个容错的区间，允许噪音数据存在（误分类样本），当松弛变量越大那么容错范围越大，反之，当ξ=0，等价于硬间隔最大化。当然我们不能无限制地容错，为了调和“间隔最大化”和“区分最大化”我们引入惩罚参数C，目标函数变成：

说明：相当于将“经验风险最小化问题”转变为引入了置信风险的“结构风险最小化问题”
说明：ξ_i≥0 与 hinge loss：max(0,1-y_i (w^T x_i+b)) 实际上是等价的。

当C 越大，模型对误分类的惩罚越大，相当于分类更精确，但同时会牺牲间隔距离，可能导致过拟合。
当C 越小，模型对误分类的惩罚越少，相当于更倾向于间隔距离最大化以提升泛化能力，但同时牺牲了分割性，可能导致欠拟合。

构造广义拉格朗日函数

阅读全文 →

日志

Softmax 回归

Softmax 回归是一种基于监督学习的分类算法，它是逻辑回归在多分类上的推广。它通过 Softmax 将线性输出层的结果进行归一化，分别表示不同分类的概率，并且所有概率之和为1。
Pasted

Softmax 回归假设式（hypothesis）：

其中 z 是线性输出层 即 z = wX + b

交叉熵（cross-entropy）:

其中p表示真实概率分布，q表示非真实概率分布;交叉熵可用于衡量真实标记的分布与预测标记的分布的差异程度。

Softmax 以交叉熵作为损失函数：

其中 m 表示样本数，k 表示分类数，如果某样本属于第 k 类，则 y_k =1，其余情况为0，h_k 表示某样本属于第 k 类的概率。

梯度计算:

解释：模型误差相对于第 k 类的第 j 个特征的权重的梯度 =（样本属于第 k 类的概率 – 该样本是否属于第k类（0或1）） x 样本第 j 个特征的值。

例如: 某样本（x1, x2, x3）标记为第2类

Pasted

什么时候用逻辑回归、什么时候用Softmax回归？

如果类别是互斥的，用Softmax，例如：香蕉、苹果、西瓜；
如果类别不互斥的，用多个逻辑回归，例如：黑白图片、户外图片、包含人的图片

转载请注明出处:

© http://hejunhao.me

日志

逻辑回归（Logistics Regression）

逻辑回归是一种有监督的分类模型(离散型输出)，它将线性函数的线性输出通过 Sigmoid 变换映射到 0~1 的范围，表示对应特征与对应输出的一种概率关系。逻辑回归本质上是一种广义线性模型，Sigmoid 只是非线性激活函数。
Pasted

二分类

例子：根据医学指标特征来判断一个人是否患有癌症。
备注：输入数据服从高斯分布，输出数据服从伯努利分布（0-1分布）。

逻辑回归假设式（hypothesis）

其中z 是线性输出层，即 z = wX+b
Sigmoid 函数的导数可以用自身来表示：h(z)’=h(z)(1-h(z))

最大似然估计(MLE)：

逻辑回归利用已知的试验结果，反推最有可能（最大概率）导致这样结果的参数值。
Pasted

逻辑回归以对数似然损失作为损失函数（log loss）

Pasted


即在样本X的前提下，使得真实分类结果Y发生的概率最大时，损失最小。
备注：逻辑回归的平方损失函数为非凸函数，存在多个局部最优解，故不采用。

损失函数（Cost Function）：

Pasted


Pasted

当 y=1 时，预测为正例的概率(即h(x))越大，模型的损失就越低，当h(x) = 1，即100%认为是正例时，模型损失最低，cost=0，表示完全预测正确.

Pasted

当 y=0 时，预测为正例的概率越大，模型的损失就越大，当h(x)=1,即100%认为是正例时，模型的损失趋向无穷大，表示完全预测错误。
合并损失函数多行式：

Pasted

最终的损失函数形式为：

除了假设式h(x) 不同，偏导结果与线性回归完全一致。

多分类 – 多个逻辑回归

One vs all (One vs rest):

将多分类问题看成多个独立的二分类问题，例如有A、B、C三个分类，那么训练以下三个分类器：
a) 将训练样本中A分类标记为1，其他标记为0，训练一个能识别是不是A的分类器
b) 将训练样本中B分类标记为1，其他标记为0，训练一个能识别是不是B的分类器
c) 将训练样本中C分类标记为1，其他标记为0，训练一个能识别是不是C的分类器

对于新的输入特征X，通过以上三个分类器进行预测，选择预测概率最大的那个分类器对应的分类作为预测的结果。

转载请注明出处:

© http://hejunhao.me

第 2 页，共 3 页123